Solve the inequality for y: y + 6 ≤ -5
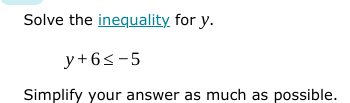
Understand the Problem
The question asks to solve the inequality y + 6 ≤ -5 for y and simplify the answer as much as possible. This involves isolating y on one side of the inequality.
Answer
$y \le -11$
Answer for screen readers
$y \le -11$
Steps to Solve
- Isolate $y$ by subtracting 6 from both sides of the inequality
To solve the inequality $y + 6 \le -5$, we need to isolate $y$ on one side. We can do this by subtracting 6 from both sides of the inequality: $$y + 6 - 6 \le -5 - 6$$
- Simplify both sides of the inequality
Simplifying both sides, we get: $$y \le -11$$
$y \le -11$
More Information
The solution to the inequality $y + 6 \le -5$ is $y \le -11$. This means any value of $y$ that is less than or equal to $-11$ will satisfy the original inequality. For instance, if $y = -12$, then $-12 + 6 = -6$, which is less than $-5$.
Tips
A common mistake is forgetting to subtract 6 from both sides of the inequality. Another mistake is to change the direction of the inequality sign when it's not necessary. The direction of the inequality sign only needs to be changed when multiplying or dividing both sides by a negative number, which is not the case here.
AI-generated content may contain errors. Please verify critical information