Simplify: $\left(-\frac{3}{5}\right)^4 \times \left(\frac{4}{9}\right)^4 \times \left(-\frac{5}{8}\right)^2$
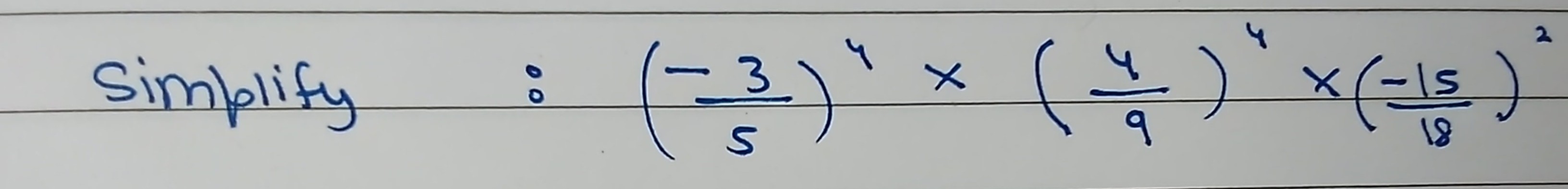
Understand the Problem
The question asks to simplify an expression involving fractions raised to different powers. We need to evaluate each term separately and then multiply them together.
Answer
$\frac{4}{2025}$
Answer for screen readers
$\frac{4}{2025}$
Steps to Solve
-
Evaluate the first term Since the exponent is even, the negative sign will disappear. $\left(-\frac{3}{5}\right)^4 = \frac{(-3)^4}{5^4} = \frac{81}{625}$
-
Evaluate the second term $\left(\frac{4}{9}\right)^4 = \frac{4^4}{9^4} = \frac{256}{6561}$
-
Evaluate the third term Since the exponent is even, the negative sign will disappear. $\left(-\frac{5}{8}\right)^2 = \frac{(-5)^2}{8^2} = \frac{25}{64}$
-
Multiply the simplified terms $\frac{81}{625} \times \frac{256}{6561} \times \frac{25}{64} = \frac{81 \times 256 \times 25}{625 \times 6561 \times 64}$
-
Simplify the expression $\frac{81 \times 256 \times 25}{625 \times 6561 \times 64} = \frac{81}{6561} \times \frac{256}{64} \times \frac{25}{625} = \frac{1}{81} \times 4 \times \frac{1}{25} = \frac{4}{81 \times 25} = \frac{4}{2025}$
$\frac{4}{2025}$
More Information
The result is a fraction. We simplified each term with exponents individually before multiplying everything together.
Tips
A common mistake is not recognizing that a negative number raised to an even power becomes positive. Also, students may make calculation errors when dealing with larger numbers.
AI-generated content may contain errors. Please verify critical information