Solve the following systems of equations graphically: a) x + y = 3 ; x - y = 1 b) x + 2y = 2 ; 2x + 5y = 2
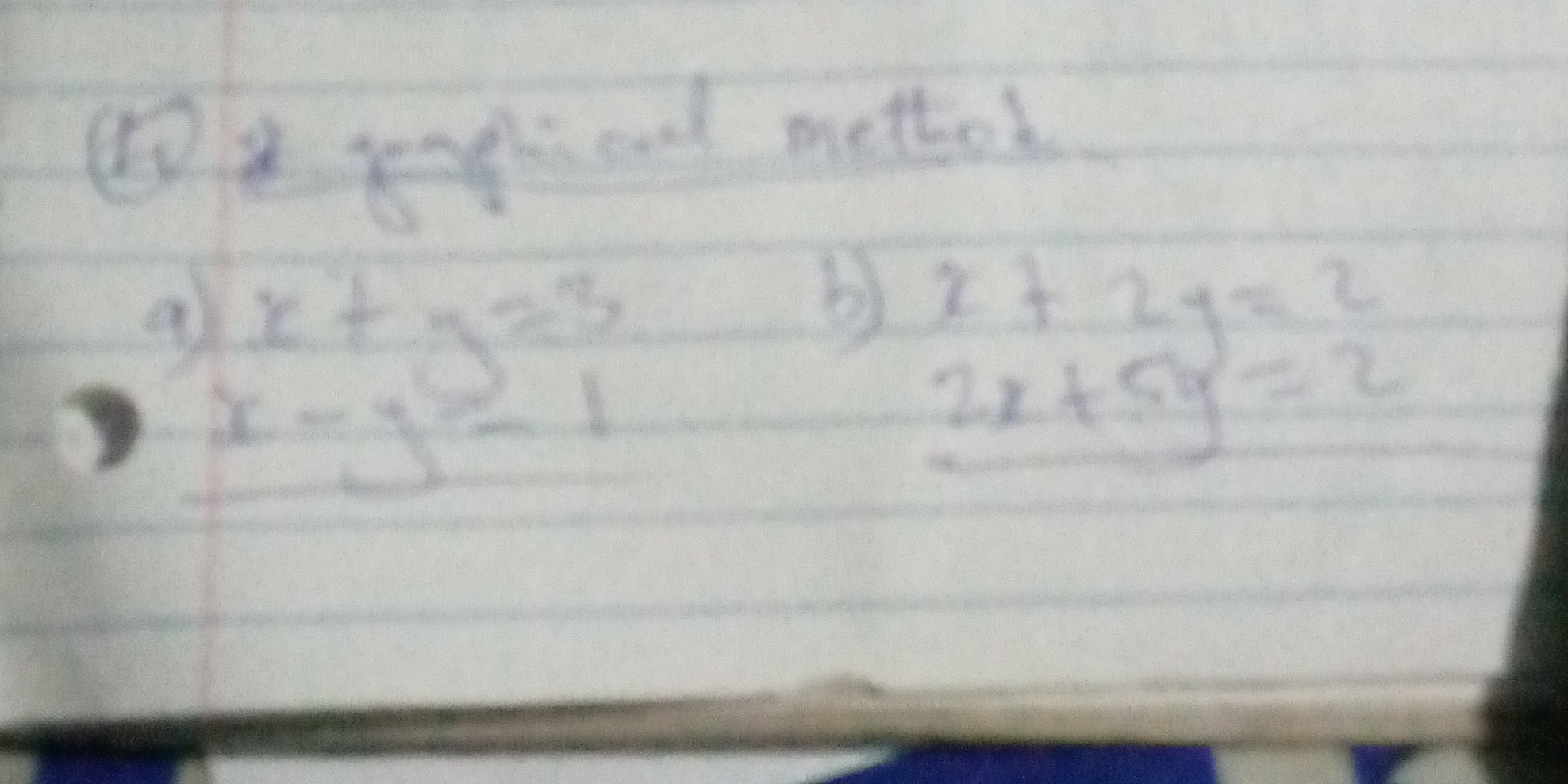
Understand the Problem
The question asks to solve the following systems of linear equations using the graphical method: a) x + y = 3 and x - y = 1 b) x + 2y = 2 and 2x + 5y = 2
Answer
a) $x = 2$, $y = 1$ b) $x = 6$, $y = -2$
Answer for screen readers
a) $x = 2$, $y = 1$ b) $x = 6$, $y = -2$
Steps to Solve
-
Solve for y in terms of x for each equation in system a)
- For $x + y = 3$, subtract $x$ from both sides to get $y = 3 - x$.
- For $x - y = 1$, subtract $x$ from both sides to get $-y = 1 - x$, then multiply both sides by $-1$ to get $y = x - 1$.
-
Find two points for each equation in system a)
-
For $y = 3 - x$: If $x = 0$, then $y = 3 - 0 = 3$. Point 1: $(0, 3)$. If $x = 3$, then $y = 3 - 3 = 0$. Point 2: $(3, 0)$.
-
For $y = x - 1$: If $x = 0$, then $y = 0 - 1 = -1$. Point 3: $(0, -1)$. If $x = 1$, then $y = 1 - 1 = 0$. Point 4: $(1, 0)$.
-
-
Plot the lines for system a) and find the intersection point
- Plot the points and draw the lines for $y = 3 - x$ and $y = x - 1$. The intersection point of these two lines is the solution to the system. The lines intersect at $(2, 1)$.
-
Solve for y in terms of x for each equation in system b)
- For $x + 2y = 2$, subtract $x$ from both sides to get $2y = 2 - x$, then divide both sides by $2$ to get $y = 1 - \frac{1}{2}x$.
- For $2x + 5y = 2$, subtract $2x$ from both sides to get $5y = 2 - 2x$, then divide both sides by $5$ to get $y = \frac{2}{5} - \frac{2}{5}x$.
-
Find two points for each equation in system b)
-
For $y = 1 - \frac{1}{2}x$: If $x = 0$, then $y = 1 - \frac{1}{2}(0) = 1$. Point 1: $(0, 1)$. If $x = 2$, then $y = 1 - \frac{1}{2}(2) = 0$. Point 2: $(2, 0)$.
-
For $y = \frac{2}{5} - \frac{2}{5}x$: If $x = 1$, then $y = \frac{2}{5} - \frac{2}{5}(1) = 0$. Point 3: $(1,0)$. If $x = -4$, then $y = \frac{2}{5} - \frac{2}{5}(-4) = 2$. Point 4: $(-4, 2)$.
-
-
Plot the lines for system b) and find the intersection point
- Plot the points and draw the lines for $y = 1 - \frac{1}{2}x$ and $y = \frac{2}{5} - \frac{2}{5}x$. The intersection point of these two lines is the solution to the system. The lines intersect at $(6, -2)$.
a) $x = 2$, $y = 1$ b) $x = 6$, $y = -2$
More Information
The graphical method involves plotting the equations on a graph and finding the point where the lines intersect. This intersection point represents the solution to the system of equations, as it satisfies both equations simultaneously.
Tips
- Incorrectly plotting the points or drawing the lines, leading to a wrong intersection point.
- Algebraic errors when solving for $y$ in terms of $x$.
- Misreading the graph to determine the coordinates of the intersection point.
AI-generated content may contain errors. Please verify critical information