Solve the following system of equations: x + 2y = 2 2x + 5y = 2
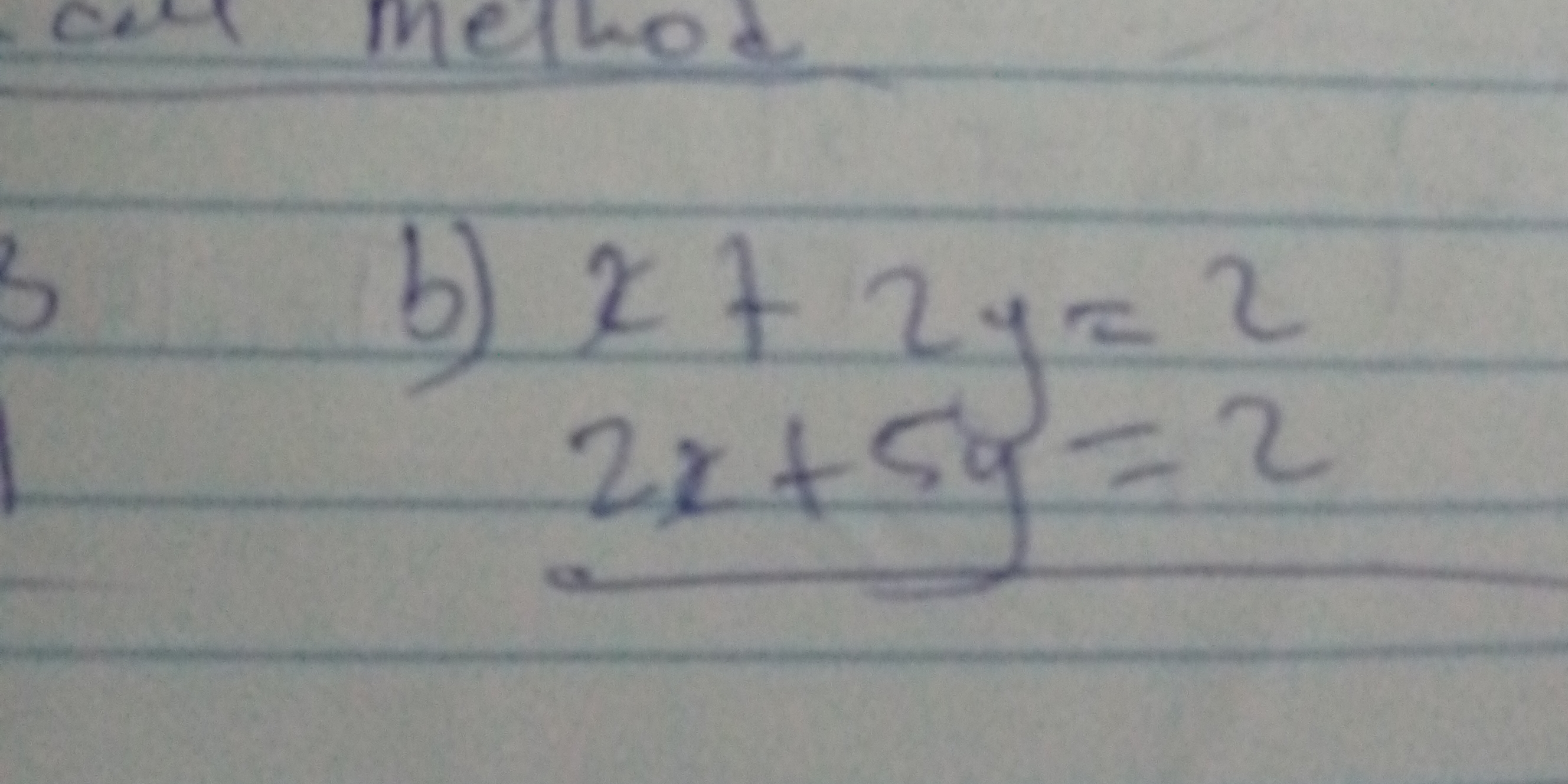
Understand the Problem
The question requires solving a system of two linear equations with two variables, x and y. We need to find the values of x and y that satisfy both equations simultaneously.
Answer
$x = 6$, $y = -2$
Answer for screen readers
$x = 6$ and $y = -2$
Steps to Solve
-
Multiply the first equation by -2 This will allow us to eliminate $x$ when we add the two equations together. $$ -2(x + 2y) = -2(2) $$ $$ -2x - 4y = -4 $$
-
Add the modified first equation to the second equation This eliminates $x$ and leaves an equation in terms of $y$. $$ (-2x - 4y) + (2x + 5y) = -4 + 2 $$ $$ y = -2 $$
-
Substitute the value of $y$ into the first equation We use the value we obtained for $y$ to compute $x$. $$ x + 2(-2) = 2 $$ $$ x - 4 = 2 $$
-
Solve for $x$ Isolate x by adding 4 to both sides of the equation. $$ x = 2 + 4 $$ $$ x = 6 $$
$x = 6$ and $y = -2$
More Information
We can check our answer by substituting these values back into the original equations:
First equation: $$ x + 2y = 6 + 2(-2) = 6 - 4 = 2 $$ Second equation: $$ 2x + 5y = 2(6) + 5(-2) = 12 - 10 = 2 $$ Both equations are satisfied, so our solution is correct.
Tips
A common mistake is to make an arithmetic error when solving for x or y, especially when dealing with negative signs. Always double-check your work by substituting the values back into the original equations.
AI-generated content may contain errors. Please verify critical information