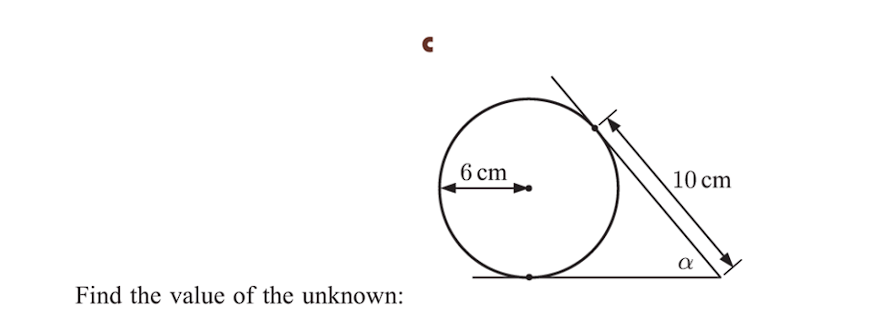
Find the value of angle α given a circle with radius 3 cm and a tangent of length 10 cm to the circle.
Understand the Problem
The question requires finding the value of the unknown angle α in a geometric diagram involving a circle and tangents. Given the radius of the circle (6 cm) = 6/2 = 3 cm which is 3 cm and the length of the tangent segment (10 cm), we can use trigonometric relationships to determine the measure of angle α. We can use the tangent property that states that the tangent line is perpendicular to the radius at the point of tangency to form a right triangle, allowing us to use trigonometric functions.
Answer
$\alpha \approx 30.96^{\circ}$
Answer for screen readers
$\alpha \approx 30.96^{\circ}$
Steps to Solve
-
Identify the Right Triangle The tangent to the circle is perpendicular to the radius at the point of tangency. This forms a right triangle.
-
Identify Given Sides We have the length of the opposite side to the angle $\alpha$, which is the radius of the circle $r = 6 \text{ cm}$. We also know the length of the adjacent side to the angle $\alpha$, which is the tangent segment $t = 10 \text{ cm}$.
-
Use the Tangent Function The tangent of an angle in a right triangle is the ratio of the opposite side to the adjacent side. Therefore: $$ \tan(\alpha) = \frac{\text{opposite}}{\text{adjacent}} = \frac{r}{t} $$
-
Substitute the Given Values Plug in the values of the radius and the tangent segment: $$ \tan(\alpha) = \frac{6}{10} = 0.6 $$
-
Find the Angle $\alpha$ To find the value of $\alpha$, we take the inverse tangent (arctan) of 0.6: $$ \alpha = \arctan(0.6) $$
-
Calculate the arctangent $$ \alpha \approx 30.96^{\circ} $$
$\alpha \approx 30.96^{\circ}$
More Information
The angle $\alpha$ is approximately $30.96$ degrees. This angle is formed by the tangent segment and the line connecting the point of tangency to the center of the circle.
Tips
A common mistake is using the wrong trigonometric function (e.g., sine or cosine) or using the incorrect sides of the triangle in the ratio. Always remember SOH CAH TOA to ensure you are using the right ratio. Also, make sure your calculator is in degree mode when finding the inverse tangent.
AI-generated content may contain errors. Please verify critical information