Solve the following problems: 1) Solve the system of equations using substitution: 2r - t = 7 r - t = 1 2) True or false: The system of equations has infinite solutions: x + 5y =... Solve the following problems: 1) Solve the system of equations using substitution: 2r - t = 7 r - t = 1 2) True or false: The system of equations has infinite solutions: x + 5y = 2 10y = -2x+4
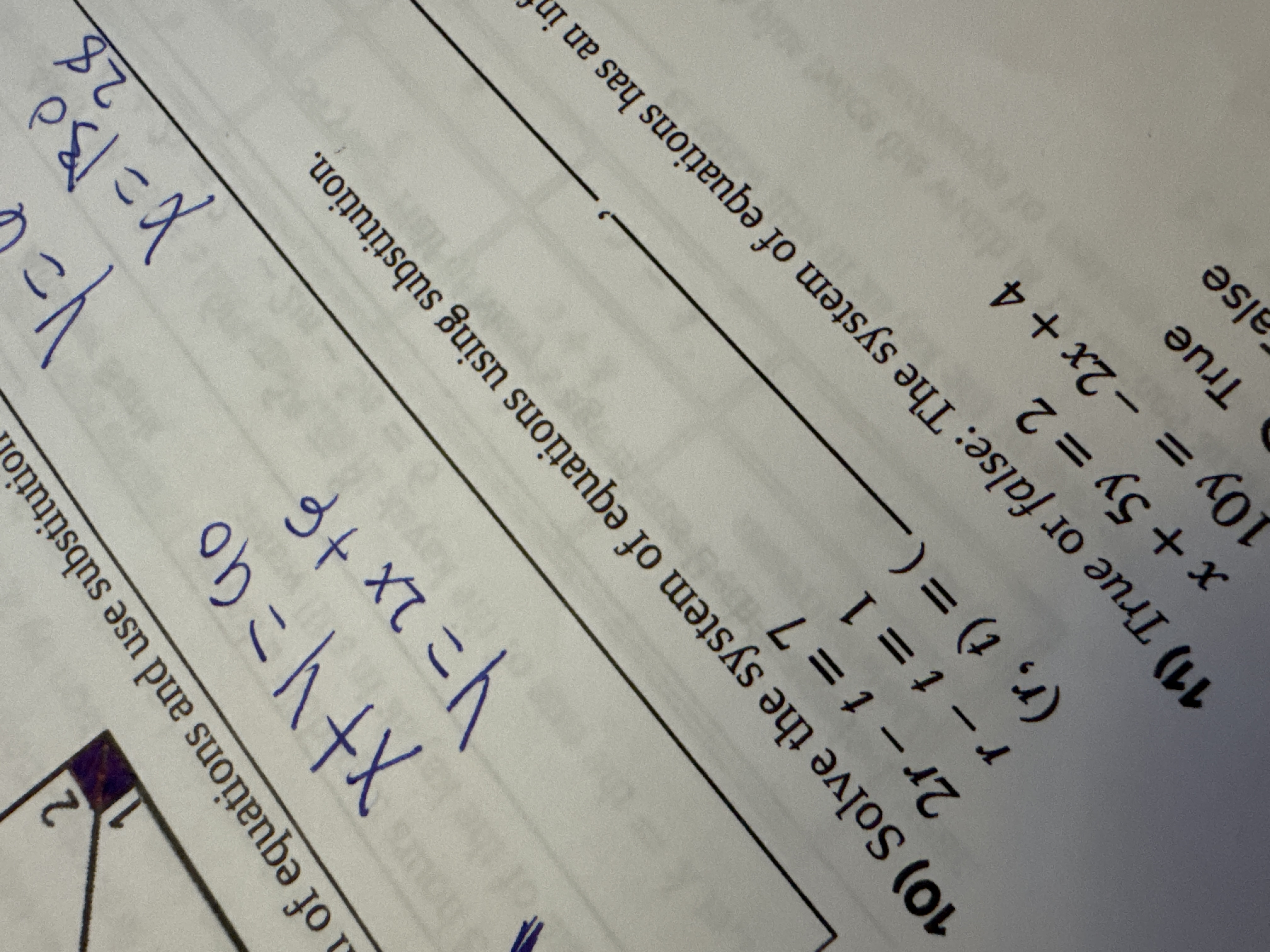
Understand the Problem
There are two math problems included in the image. One of them asks to solve a system of linear equations with two variables using substitution. The system is:
2r - t = 7 r - t = 1
The goal is to find the values of 'r' and 't' that satisfy both equations.
The second problem tests whether the following equations have infinite solutions. x + 5y = 2 10y = -2x+4
Answer
(6, 5) True
Answer for screen readers
(6, 5) True
Steps to Solve
- Solve for $t$ in the second equation
We are given the equation $r - t = 1$. To solve for $t$, we can add $t$ to both sides and subtract $1$ from both sides. This gives us $r - 1 = t$, or $t = r - 1$.
- Substitute $t$ into the first equation
The first equation is $2r - t = 7$. We substitute $t = r - 1$ into this equation to get $2r - (r - 1) = 7$.
- Solve for $r$
Simplifying the equation $2r - (r - 1) = 7$, we get $2r - r + 1 = 7$, which simplifies to $r + 1 = 7$. Subtracting $1$ from both sides gives us $r = 6$.
- Solve for $t$
Now that we have $r = 6$, we can substitute this value back into the equation $t = r - 1$. This gives us $t = 6 - 1$, so $t = 5$.
- State the solution for the first system
The solution to the system of equations is $r = 6$ and $t = 5$. So the ordered pair is $(6, 5)$.
- Analyze the second system of equations
We have the system: $x + 5y = 2$ $10y = -2x + 4$
Let's rearrange the second equation to match the form of the first equation: Add $2x$ to both sides: $2x + 10y = 4$ Divide the entire equation by 2: $x + 5y = 2$
- Determine if infinite solutions exist
Since both equations are equivalent ($x + 5y = 2$), the system has infinitely many solutions. Therefore, the statement is true.
(6, 5) True
More Information
A system of equations has infinite solutions when the two equations represent the same line. In other words, one equation is a multiple of the other.
Tips
A common mistake would be to forget to distribute the negative sign when substituting $t = r-1$ into the first equation. It's important to remember that $2r - (r - 1)$ becomes $2r - r + 1$, not $2r - r - 1$. Another common mistake is not rearranging the second equation in the second part to be in the same format as the first.
AI-generated content may contain errors. Please verify critical information