Solve the equation: (x² - 3x + 1)^(2x² + x - 6) = 1
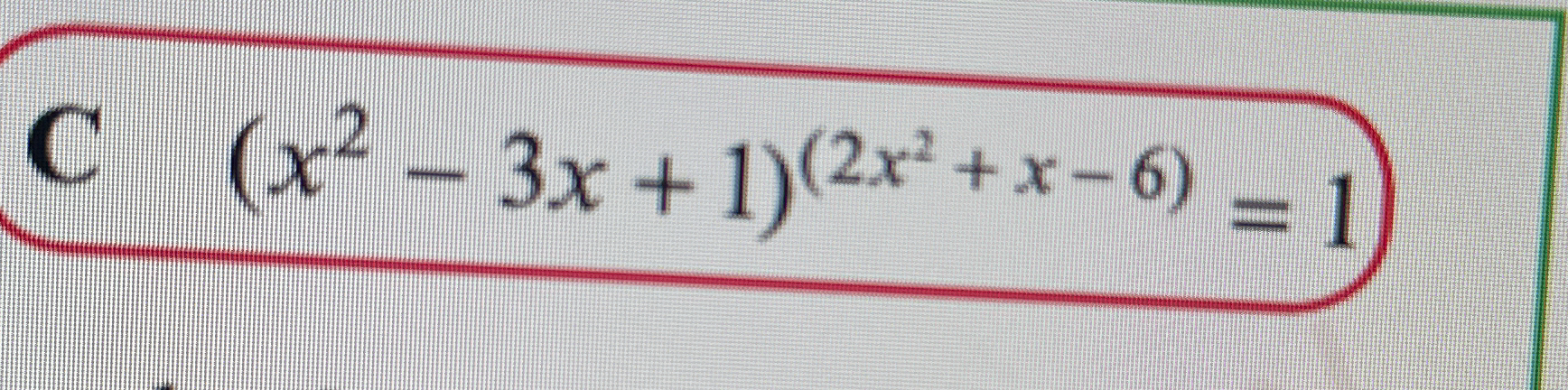
Understand the Problem
The question asks to solve the equation: (x² - 3x + 1)^(2x² + x - 6) = 1. This involves finding the values of x that satisfy the equation where a polynomial expression raised to another polynomial expression equals 1.
Answer
$x = -2, 0, \frac{3}{2}, 2, 3$
Answer for screen readers
$x = -2, 0, \frac{3}{2}, 2, 3$
Steps to Solve
-
Identify cases where the equation holds true. The equation $a^b = 1$ is true in three scenarios:
- $a = 1$ (base is 1)
- $b = 0$ and $a \ne 0$ (exponent is 0)
- $a = -1$ and $b$ is an even integer (base is -1 and exponent is even)
-
Solve for when the base equals 1. Set the base equal to 1 and solve for x: $x^2 - 3x + 1 = 1$ $x^2 - 3x = 0$ $x(x - 3) = 0$ $x = 0$ or $x = 3$
-
Solve for when the exponent equals 0. Set the exponent equal to 0 and solve for x: $2x^2 + x - 6 = 0$ $(2x - 3)(x + 2) = 0$ $x = \frac{3}{2}$ or $x = -2$ Check that the base is not 0 for these values of x: If $x = \frac{3}{2}$, the base is $(\frac{3}{2})^2 - 3(\frac{3}{2}) + 1 = \frac{9}{4} - \frac{9}{2} + 1 = \frac{9 - 18 + 4}{4} = -\frac{5}{4} \ne 0$ If $x = -2$, the base is $(-2)^2 - 3(-2) + 1 = 4 + 6 + 1 = 11 \ne 0$ Thus, $x = \frac{3}{2}$ and $x = -2$ are valid solutions.
-
Solve for when the base equals -1 and exponent is even. Set the base equal to -1 and solve for x: $x^2 - 3x + 1 = -1$ $x^2 - 3x + 2 = 0$ $(x - 1)(x - 2) = 0$ $x = 1$ or $x = 2$ Now check if the exponent is even for these values: If $x = 1$, the exponent is $2(1)^2 + 1 - 6 = 2 + 1 - 6 = -3$, which is odd, so $x = 1$ is not a solution. If $x = 2$, the exponent is $2(2)^2 + 2 - 6 = 8 + 2 - 6 = 4$, which is even, so $x = 2$ is a valid solution.
-
List all solutions. The solutions are $x = 0, 3, \frac{3}{2}, -2, 2$.
$x = -2, 0, \frac{3}{2}, 2, 3$
More Information
The problem explores the different scenarios where an expression to the power of another expression can equal 1.
Tips
A common mistake is forgetting to check if the base is non-zero when the exponent is zero, or forgetting to check if the exponent is an even integer when the base is -1.
AI-generated content may contain errors. Please verify critical information