Solve the equation 4(2x^2 + x - 6) = 1.
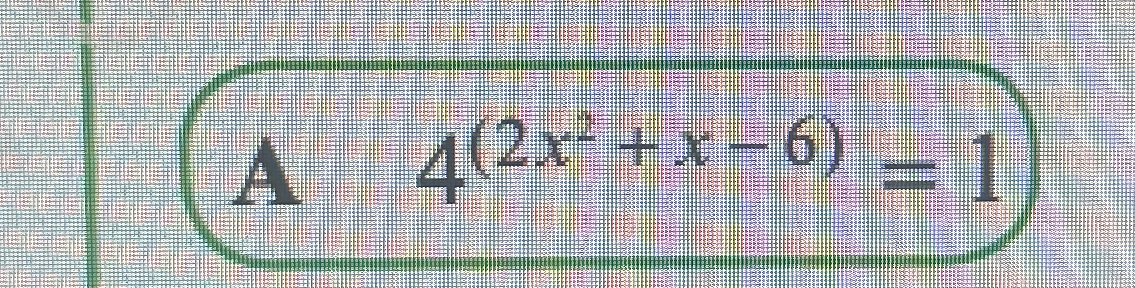
Understand the Problem
The question asks to solve the quadratic equation 4(2x^2 + x - 6) = 1 for x. This involves simplifying the equation and then using methods such as factoring, completing the square, or the quadratic formula to find the solutions.
Answer
$x = \frac{-1 \pm \sqrt{51}}{4}$
Answer for screen readers
$x = \frac{-1 \pm \sqrt{51}}{4}$
Steps to Solve
-
Distribute the 4 Multiply each term inside the parenthesis by 4: $4(2x^2 + x - 6) = 8x^2 + 4x - 24$ So the updated equation is: $8x^2 + 4x - 24 = 1$
-
Set the equation to zero Subtract 1 from both sides to set the equation to zero: $8x^2 + 4x - 24 - 1 = 1 - 1$ $8x^2 + 4x - 25 = 0$
-
Apply the quadratic formula The quadratic formula is: $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$ In this case, $a = 8$, $b = 4$, and $c = -25$. Plug these values into the quadratic formula: $x = \frac{-4 \pm \sqrt{4^2 - 4(8)(-25)}}{2(8)}$
-
Simplify the expression Simplify the terms under the square root: $x = \frac{-4 \pm \sqrt{16 + 800}}{16}$ $x = \frac{-4 \pm \sqrt{816}}{16}$
-
Simplify the square root Simplify the square root by factoring out perfect squares. $\sqrt{816}=\sqrt{16 \cdot 51} = 4\sqrt{51}$ $x = \frac{-4 \pm 4\sqrt{51}}{16}$
-
Reduce the fraction by dividing by the greatest common factor Divide all coefficients by 4: $x = \frac{-1 \pm \sqrt{51}}{4}$
$x = \frac{-1 \pm \sqrt{51}}{4}$
More Information
The solutions to the quadratic equation are $x = \frac{-1 + \sqrt{51}}{4}$ and $x = \frac{-1 - \sqrt{51}}{4}$. These are the exact solutions. Approximations can be found using a calculator if needed.
Tips
- Incorrectly applying the quadratic formula: A common mistake is to incorrectly substitute the values of a, b, and c into the quadratic formula, or to make errors in the arithmetic when simplifying.
- Not setting the equation to zero: The quadratic formula (or factoring) can only be applied when the quadratic equation is in the standard form of $ax^2 + bx + c = 0$. Forgetting to set the equation to zero is a common mistake.
- Arithmetic errors: When simplifying the square root or the fraction, pay close attention to avoid making mistakes in arithmetic.
AI-generated content may contain errors. Please verify critical information