Solve for x: log₄(x) = -2.5
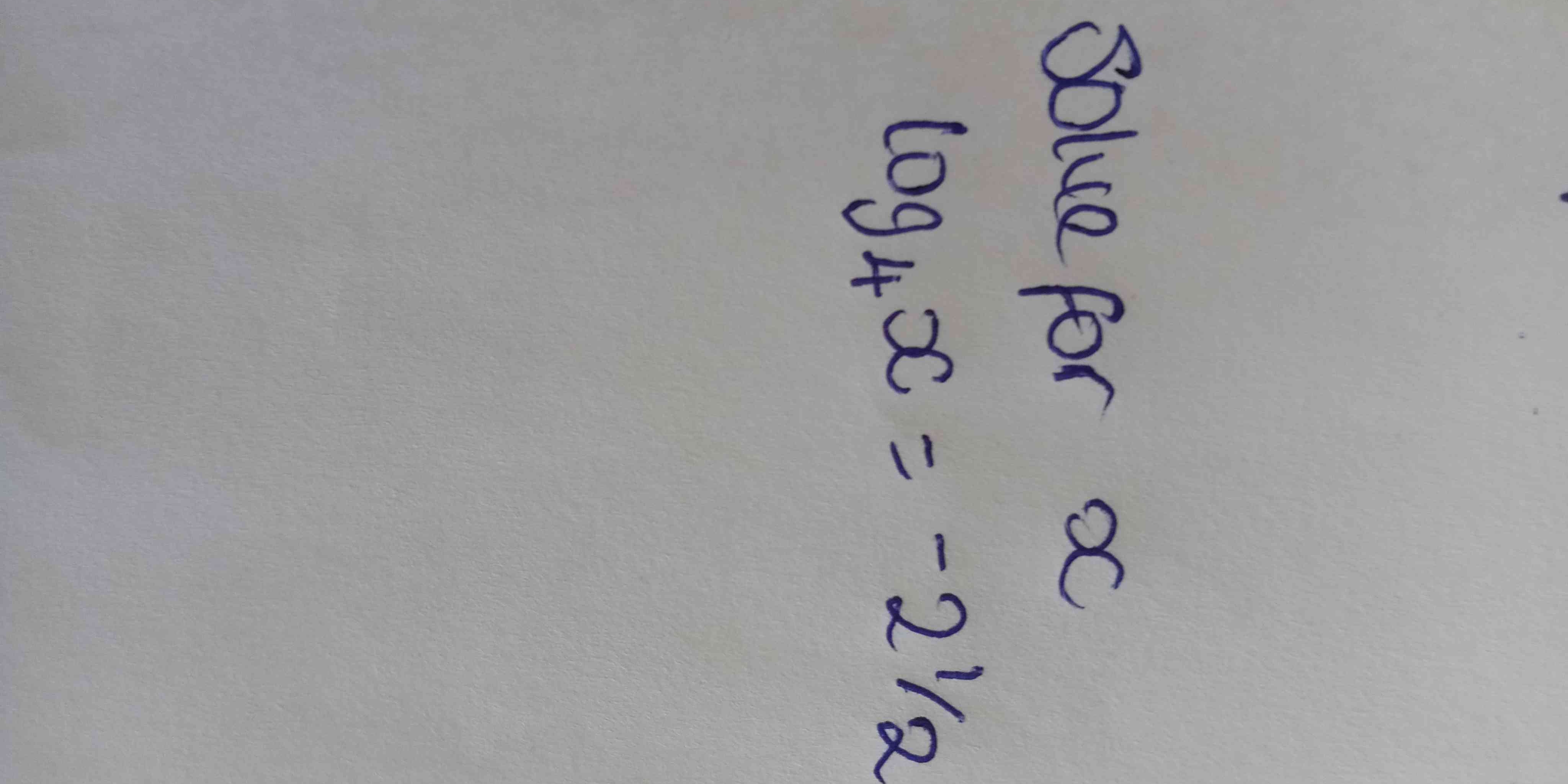
Understand the Problem
The question is asking us to solve the logarithmic equation for the variable x. To do this, we need to convert the logarithmic equation to its exponential form and then solve for x.
Answer
$x = \frac{1}{32}$
Answer for screen readers
$x = \frac{1}{32}$
Steps to Solve
-
Rewrite the mixed number as an improper fraction Rewrite $-2 \frac{1}{2}$ as $-\frac{5}{2}$. So the equation becomes $\log_4 x = -\frac{5}{2}$
-
Convert the logarithmic equation to exponential form The general form of a logarithmic equation is $\log_b a = c$, which can be converted to the exponential form $b^c = a$. In our case, $b = 4$, $a = x$, and $c = -\frac{5}{2}$. So, the exponential form of the equation is $4^{-\frac{5}{2}} = x$.
-
Simplify the exponential expression Rewrite $4$ as $2^2$, so $x = (2^2)^{-\frac{5}{2}}$. Using the power of a power rule, we get $x = 2^{2 \cdot (-\frac{5}{2})} = 2^{-5}$. Now, simplify $2^{-5}$ as $x = \frac{1}{2^5} = \frac{1}{32}$.
$x = \frac{1}{32}$
More Information
The solution to the logarithmic equation $\log_4 x = -2 \frac{1}{2}$ is $x = \frac{1}{32}$. This means that $4^{-2.5} = \frac{1}{32}$.
Tips
A common mistake is incorrectly converting between logarithmic and exponential forms. Another mistake is misinterpreting and miscalculating negative exponents. Also, one might make a mistake calculating the fraction.
AI-generated content may contain errors. Please verify critical information