Solve for x and y in the given angle equations.

Steps to Solve

1. Identify Relevant Angles in the Diagram

   In the diagram, look for angles that either share a vertex and are adjacent or are across from each other (vertical angles). This will help set up equations involving the variable ( x ).

2. Set Up Equations Using Angle Properties

   For each intersection, the angles must satisfy properties like supplementary angles (sum to ( 180^\circ )) or vertical angles (are equal).

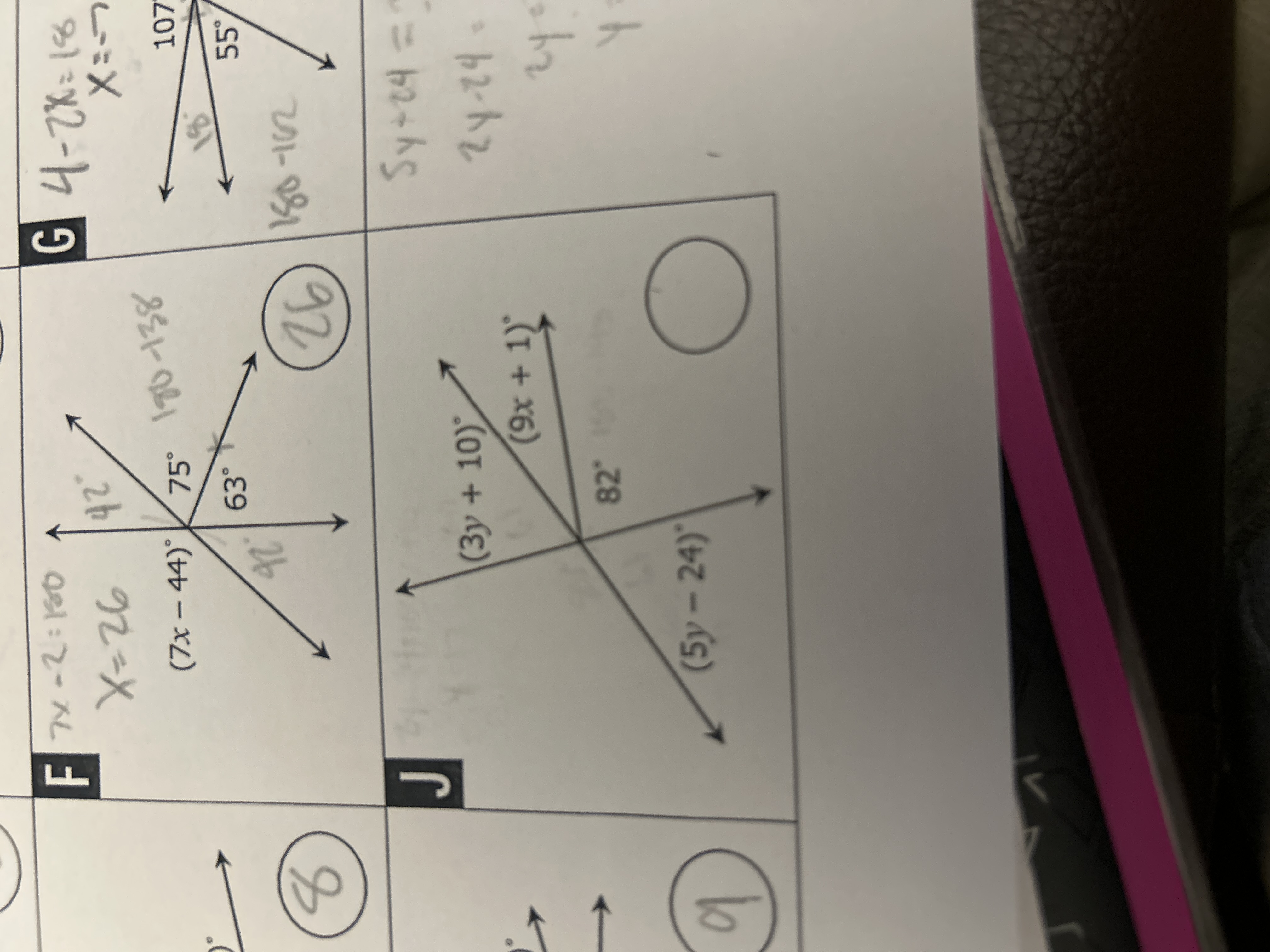
   In the problem for section J, the angles ( (3y + 10)^\circ ) and ( (9x + 1)^\circ ) are vertical angles, which means: $$ 3y + 10 = 9x + 1 $$

3. Rearrange the Equation

   Rearrange the equation to group like terms: $$ 3y = 9x + 1 - 10 $$ Simplifying gives: $$ 3y = 9x - 9 $$

4. Express ( y ) in terms of ( x )

   To isolate ( y ), divide the entire equation by 3: $$ y = 3x - 3 $$

5. Set Up Another Equation Using Other Angles

   For the other set of angles in section J, the equation formed by supplementary angles (i.e., ( (5y - 24)^\circ + 82^\circ = 180^\circ )): $$ 5y - 24 + 82 = 180 $$

6. Simplify and Solve for ( y )

   Combine the constants: $$ 5y + 58 = 180 $$ Now subtract 58 from both sides: $$ 5y = 122 $$

   Divide by 5 to find ( y ): $$ y = \frac{122}{5} = 24.4 $$

7. Substitute ( y ) Back to Find ( x )

   Substitute ( y ) back into the equation derived for ( y ): $$ 24.4 = 3x - 3 $$ Rearranging gives: $$ 3x = 24.4 + 3 = 27.4 $$ Dividing gives: $$ x = \frac{27.4}{3} \approx 9.1333 $$