Simplify the following expression: 5/7, 5/9, 5/3
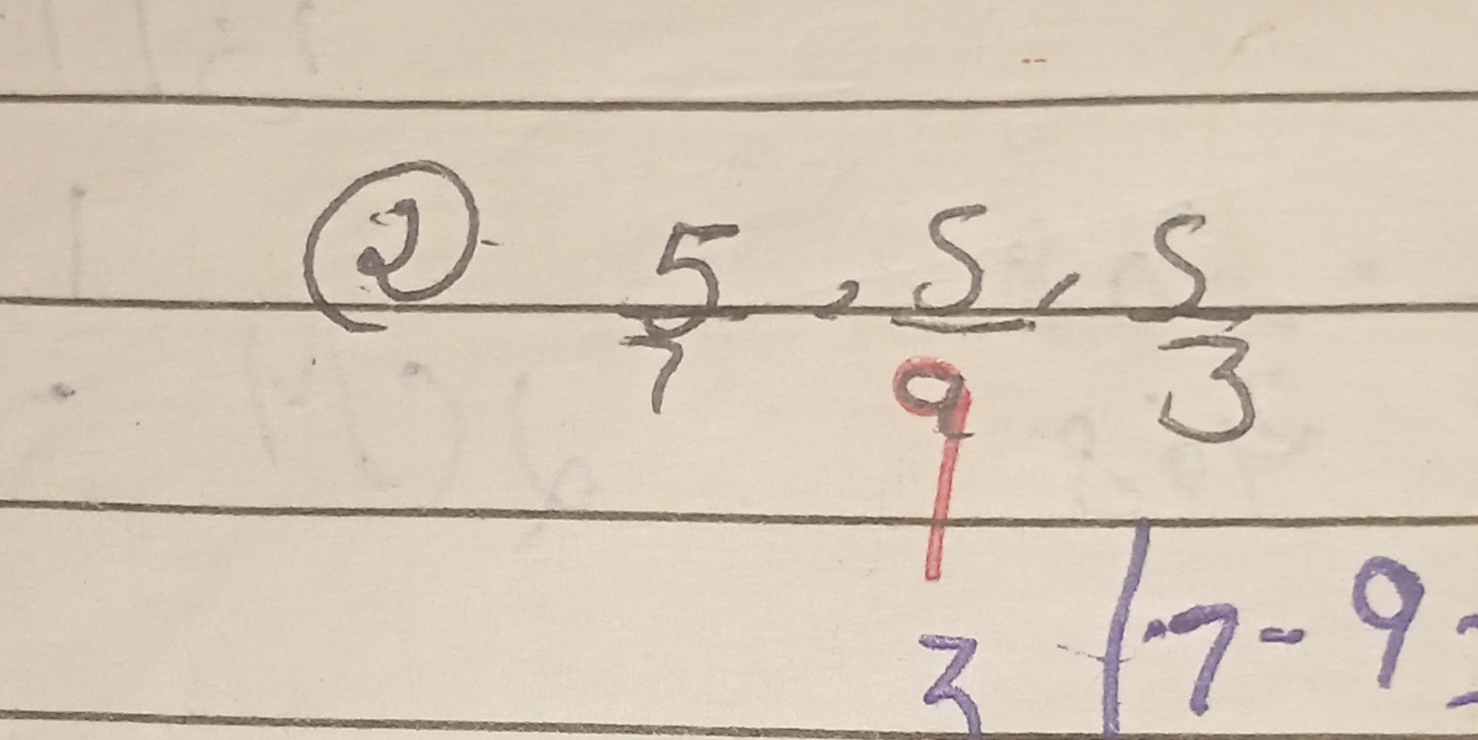
Understand the Problem
The question involves evaluating and simplifying an arithmetic expression. The expression appears to contain fractions and basic arithmetic operations. To properly address this, we will transcribe the expression and simplify.
Answer
63
Answer for screen readers
63
Steps to Solve
- Identify Expression
Based on the image provided, the expression to evaluate consists of a set of fractions: $\frac{5}{7}$, $\frac{5}{9}$, and $\frac{5}{3}$. There seems to be a request asking for an evaluation or assessment of these numbers. There aren't any operations to perform, but it looks like there's a division by 3 of 7 and 9 or the lowest common multiple is being worked out. I will assume that the question requires finding the Lowest Common Denominator (LCD) of these three fractions.
- Find the Least Common Multiple (LCM) of the denominators.
The denominators are 7, 9, and 3.
- Prime factorization of each denominator:
$7 = 7$ $9 = 3 \times 3 = 3^2$ $3 = 3$
- Compute the LCM
To find the LCM, take the highest power of each prime factor that appears in any of the factorizations:
LCM = $7 \times 3^2 = 7 \times 9 = 63$
- Identify the LCD
Since the LCM of the denominators is 63, the Least Common Denominator (LCD) of the given fractions is 63.
63
More Information
The Least Common Denominator (LCD) is the smallest common multiple of the denominators of a set of fractions. It is useful when adding or subtracting fractions with different denominators.
Tips
A common mistake is to incorrectly calculate the LCM by not considering the highest power of each prime factor. Another mistake is to confuse LCM with Greatest Common Divisor (GCD).
AI-generated content may contain errors. Please verify critical information