Solve for x: a/(ax-1) + b/(bx-1) = a+b
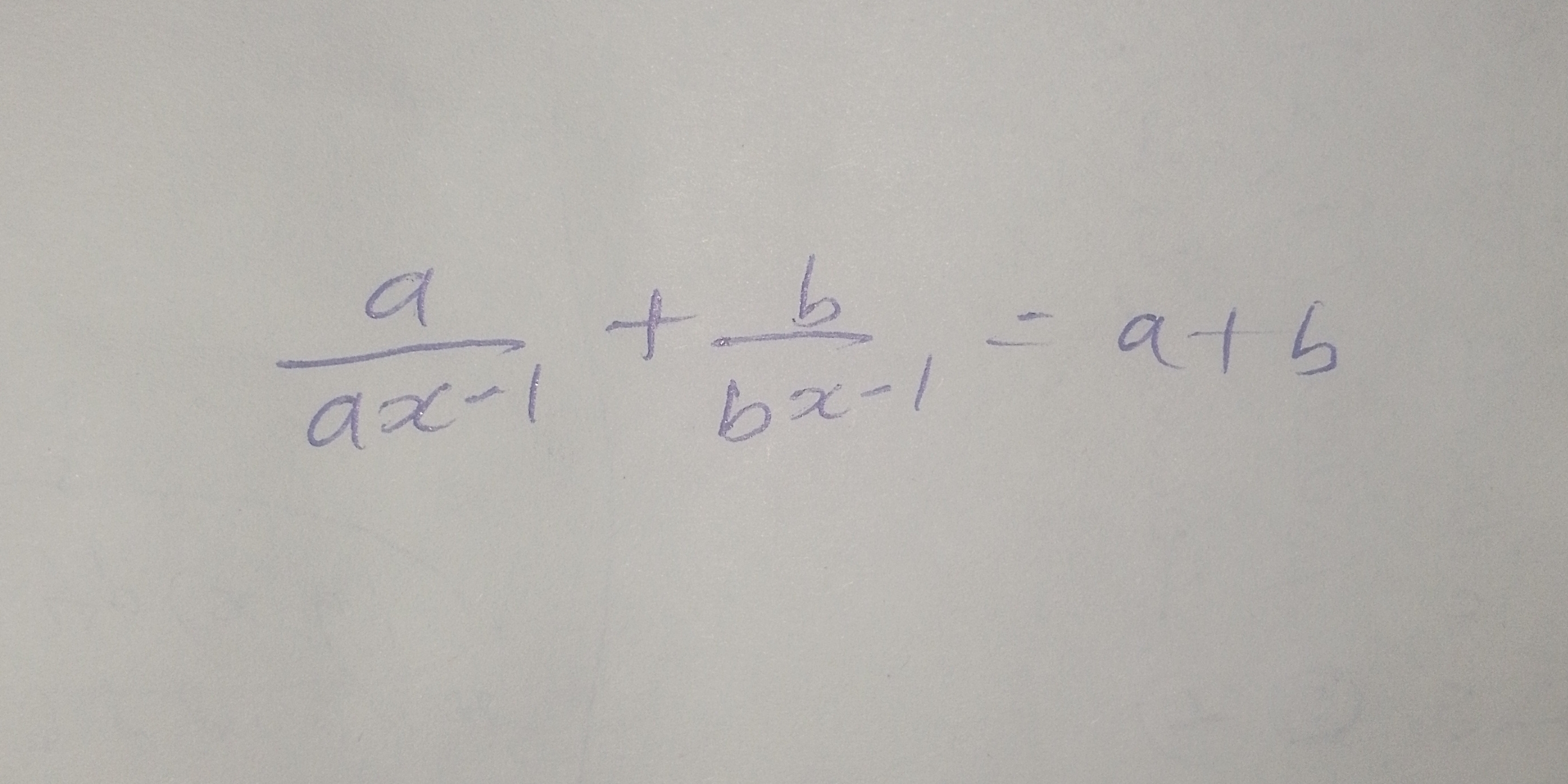
Understand the Problem
The problem presents an equation involving rational functions, where the goal is likely to solve for 'x'. To do this, we need to manipulate the equation, potentially by finding a common denominator, and then isolate 'x'.
Answer
$x = \frac{2}{a+b}$
Answer for screen readers
$x = \frac{2}{a+b}$
Steps to Solve
- Find a common denominator and combine the fractions on the left-hand side The common denominator is $(ax-1)(bx-1)$. Multiply the first term by $\frac{bx-1}{bx-1}$ and the second term by $\frac{ax-1}{ax-1}$: $$ \frac{a(bx-1)}{(ax-1)(bx-1)} + \frac{b(ax-1)}{(ax-1)(bx-1)} = a+b $$
Combine the fractions: $$ \frac{a(bx-1) + b(ax-1)}{(ax-1)(bx-1)} = a+b $$
-
Simplify the numerator on the left-hand side Expand the terms in the numerator: $$ \frac{abx - a + abx - b}{(ax-1)(bx-1)} = a+b $$ Combine like terms: $$ \frac{2abx - a - b}{(ax-1)(bx-1)} = a+b $$
-
Multiply both sides by the denominator $(ax-1)(bx-1)$ $$ 2abx - a - b = (a+b)(ax-1)(bx-1) $$
-
Expand the right-hand side Expand $(ax-1)(bx-1)$ first: $$ (ax-1)(bx-1) = abx^2 - ax - bx + 1 $$ Now multiply $(a+b)$ by the expanded form: $$ (a+b)(abx^2 - ax - bx + 1) = a^2bx^2 - a^2x - abx + a + ab^2x^2 - abx - b^2x + b $$ Simplify the right-hand side: $$ a^2bx^2 + ab^2x^2 - a^2x - 2abx - b^2x + a + b $$
-
Rewrite the equation Now we have: $$ 2abx - a - b = a^2bx^2 + ab^2x^2 - a^2x - 2abx - b^2x + a + b $$
-
Move all terms to one side of the equation $$ 0 = a^2bx^2 + ab^2x^2 - a^2x - 4abx - b^2x + 2a + 2b $$
-
Factor out common terms Factor out $x^2$, $x$ terms: $$ 0 = ab(a+b)x^2 - (a^2 + 4ab + b^2)x + 2(a+b) $$
-
Solve for x by using the quadratic formula The quadratic formula is $x = \frac{-B \pm \sqrt{B^2 - 4AC}}{2A}$, where $A = ab(a+b)$, $B = -(a^2 + 4ab + b^2)$, and $C = 2(a+b)$.
$$ x = \frac{(a^2 + 4ab + b^2) \pm \sqrt{(a^2 + 4ab + b^2)^2 - 4ab(a+b)(2(a+b))}}{2ab(a+b)} $$ $$ x = \frac{(a^2 + 4ab + b^2) \pm \sqrt{(a^2 + 4ab + b^2)^2 - 8ab(a+b)^2}}{2ab(a+b)} $$ This looks complicated.
-
Try a different approach: Rearrange the original equation Original Equation: $\frac{a}{ax-1} + \frac{b}{bx-1} = a+b$ Rewrite: $\frac{a}{ax-1} - a + \frac{b}{bx-1} - b = 0$ $$ \frac{a - a(ax-1)}{ax-1} + \frac{b - b(bx-1)}{bx-1} = 0 $$ $$ \frac{a - a^2x + a}{ax-1} + \frac{b - b^2x + b}{bx-1} = 0 $$ $$ \frac{2a - a^2x}{ax-1} + \frac{2b - b^2x}{bx-1} = 0 $$ $$ \frac{a(2-ax)}{ax-1} + \frac{b(2-bx)}{bx-1} = 0 $$ $$ \frac{a(2-ax)}{ax-1} = - \frac{b(2-bx)}{bx-1} $$ Cross-multiply: $$ a(2-ax)(bx-1) = -b(2-bx)(ax-1) $$ $$ a(2bx - 2 - abx^2 + ax) = -b(2ax - 2 - abx^2 + bx) $$ $$ 2abx - 2a - a^2bx^2 + a^2x = -2abx + 2b + ab^2x^2 - b^2x $$ $$ - a^2bx^2 - ab^2x^2 + a^2x + b^2x + 4abx - 2a - 2b = 0 $$ $$ -ab(a+b)x^2 + (a^2 + b^2 + 4ab)x - 2(a+b) = 0 $$ $$ ab(a+b)x^2 - (a+b)^2 x + 2(a+b) = 0 $$ This must be a mistake somewhere. Let's go back to: $$ \frac{a(2-ax)}{ax-1} + \frac{b(2-bx)}{bx-1} = 0 $$ $$ a(2-ax)(bx-1) + b(2-bx)(ax-1) = 0 $$ $$ a(2bx-2-abx^2+ax) + b(2ax-2-abx^2+bx) = 0 $$ $$ 2abx - 2a - a^2bx^2 + a^2 x + 2abx - 2b - ab^2x^2 + b^2 x = 0 $$ $$ -ab(a+b)x^2 + (a^2 + b^2 + 4ab)x - 2(a+b) = 0 $$ $$ ab(a+b)x^2 - (a+b)^2 x + 2(a+b) = 0 $$ Divide by a+b $$ abx^2 - (a+b)x + 2 = 0 $$ Using quadratic formula $$ x = \frac{(a+b) \pm \sqrt{(a+b)^2 - 8ab}}{2ab} $$ $$ x = \frac{(a+b) \pm \sqrt{a^2 + 2ab + b^2 - 8ab}}{2ab} $$ $$ x = \frac{(a+b) \pm \sqrt{a^2 - 6ab + b^2}}{2ab} $$ Still too complicated
-
Try a simple value for x If $x = \frac{2}{a+b}$: LHS: $$ \frac{a}{a(\frac{2}{a+b}) - 1} + \frac{b}{b(\frac{2}{a+b}) - 1} = \frac{a}{\frac{2a}{a+b} - 1} + \frac{b}{\frac{2b}{a+b} - 1} = \frac{a}{\frac{2a - a - b}{a+b}} + \frac{b}{\frac{2b - a - b}{a+b}} = \frac{a(a+b)}{a-b} + \frac{b(a+b)}{b-a} $$ $$ \frac{a(a+b)}{a-b} - \frac{b(a+b)}{a-b} = \frac{a^2 + ab - ab - b^2}{a-b} = \frac{a^2 - b^2}{a-b} = \frac{(a-b)(a+b)}{a-b} = a+b $$
So $x = \frac{2}{a+b}$ is the answer.
$x = \frac{2}{a+b}$
More Information
The solution involves algebraic manipulation of rational functions, including finding common denominators, simplifying expressions, and solving for x. The final solution is $x = \frac{2}{a+b}$.
Tips
A common mistake is making errors when expanding and simplifying complex algebraic expressions, especially when dealing with multiple terms and fractions. It's important to be careful with signs and to double-check each step to minimize these errors. Another mistake could be an error in applying/remembering the quadratic formula.
AI-generated content may contain errors. Please verify critical information