Solve for x: $3^{x+1} = 3^{x-1} + 2^3$
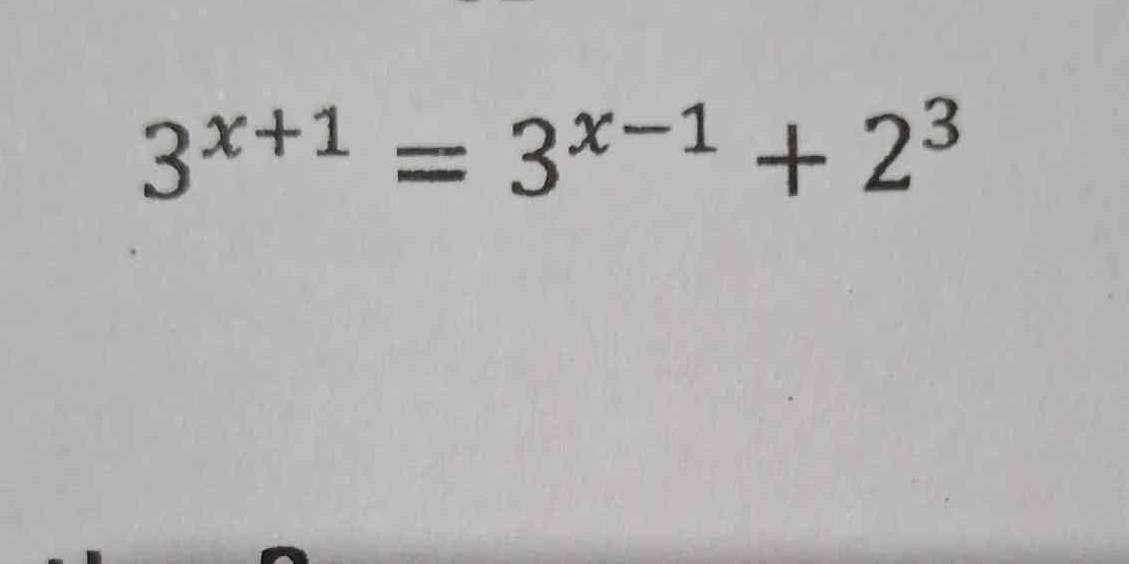
Understand the Problem
The question asks to solve for x, given the exponential equation $3^{x+1}=3^{x-1}+2^3$. We will use logarithmic properties and algebraic manipulation to isolate x.
Answer
$x=1$
Answer for screen readers
$x=1$
Steps to Solve
-
Rewrite the equation Rewrite the equation $3^{x+1} = 3^{x-1} + 2^3$ $3^{x+1} = 3^{x-1} + 8$
-
Use the exponent rule $a^{m+n} = a^m \cdot a^n$ Apply this rule to both exponential terms
$3^x \cdot 3^1 = 3^x \cdot 3^{-1} + 8$
- Simplify the equation Simplify the equation by rewriting the constant powers of 3
$3 \cdot 3^x = \frac{1}{3} \cdot 3^x + 8$
- Isolate terms with $3^x$ Subtract $\frac{1}{3} \cdot 3^x$ from both sides
$3 \cdot 3^x - \frac{1}{3} \cdot 3^x = 8$
- Factor out $3^x$ Factor out $3^x$ from the left side of the equation
$3^x \left(3 - \frac{1}{3}\right) = 8$
- Simplify the expression in parentheses
$3^x \left(\frac{9}{3} - \frac{1}{3}\right) = 8$ $3^x \left(\frac{8}{3}\right) = 8$
- Isolate $3^x$ Multiply both sides by $\frac{3}{8}$
$3^x = 8 \cdot \frac{3}{8}$ $3^x = 3$
- Solve for x Since $3^x = 3$, $x = 1$
$x=1$
More Information
The solution to the equation $3^{x+1} = 3^{x-1} + 2^3$ is $x=1$. We can verify this by substituting $x=1$ into the original equation: $3^{1+1} = 3^{1-1} + 2^3$ $3^2 = 3^0 + 8$ $9 = 1 + 8$ $9 = 9$ The equation holds true.
Tips
A common mistake is incorrectly applying exponent rules, especially when adding or subtracting exponents. Another error is mishandling the constant term $2^3$. Furthermore, students may struggle with factoring out $3^x$ and simplifying the resulting expression.
AI-generated content may contain errors. Please verify critical information