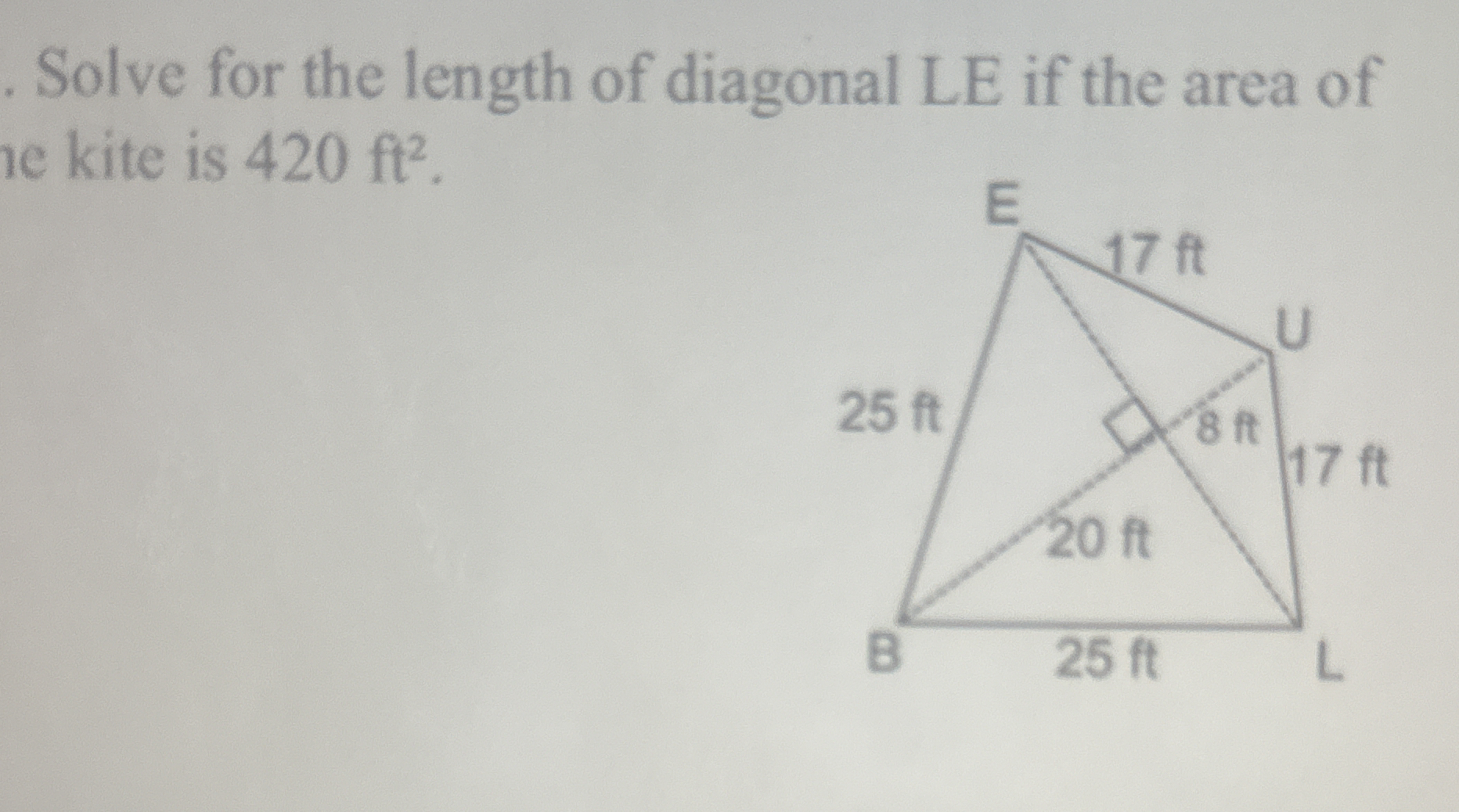
Solve for the length of diagonal LE if the area of the kite is 420 ft².
Understand the Problem
The question is asking us to determine the length of diagonal LE in a kite, given that the area is 420 square feet. We can use the formula for the area of a kite, which is A = (d1 * d2) / 2, where d1 and d2 are the lengths of the diagonals. The problem provides additional lengths that can help us find the length of the diagonal LE.
Answer
The length of diagonal LE is \(42\) ft.
Answer for screen readers
The length of diagonal LE is (42) ft.
Steps to Solve
- Identify the Formula for Area of a Kite
The formula for the area of a kite is given by:
$$ A = \frac{d_1 \cdot d_2}{2} $$
where (d_1) and (d_2) are the lengths of the diagonals.
- Set the Equation for Area
Given that the area (A) is 420 ft², we can set up the equation:
$$ 420 = \frac{d_1 \cdot d_2}{2} $$
- Multiply Both Sides by 2
To eliminate the fraction, multiply both sides of the equation by 2:
$$ 840 = d_1 \cdot d_2 $$
- Identify Known Lengths of Diagonals
From the diagram, diagonal (LU) (let's denote it as (d_1)) has a length of (20) ft. Therefore, we can substitute (d_1) into the area equation:
$$ 840 = 20 \cdot d_2 $$
- Solve for the Unknown Diagonal (d_2)
To find the length of diagonal (LE) (denote it as (d_2)), divide both sides by (20):
$$ d_2 = \frac{840}{20} = 42 \text{ ft} $$
The length of diagonal LE is (42) ft.
More Information
Kites have two diagonals that intersect at right angles, and their area can be easily calculated using the lengths of these diagonals. Here, one diagonal was given, enabling us to calculate the second.
Tips
- Forgetting to multiply by 2 when starting from the area formula.
- Misidentifying the diagonals' lengths from the diagram, which can lead to incorrect substitution in the area formula.
AI-generated content may contain errors. Please verify critical information