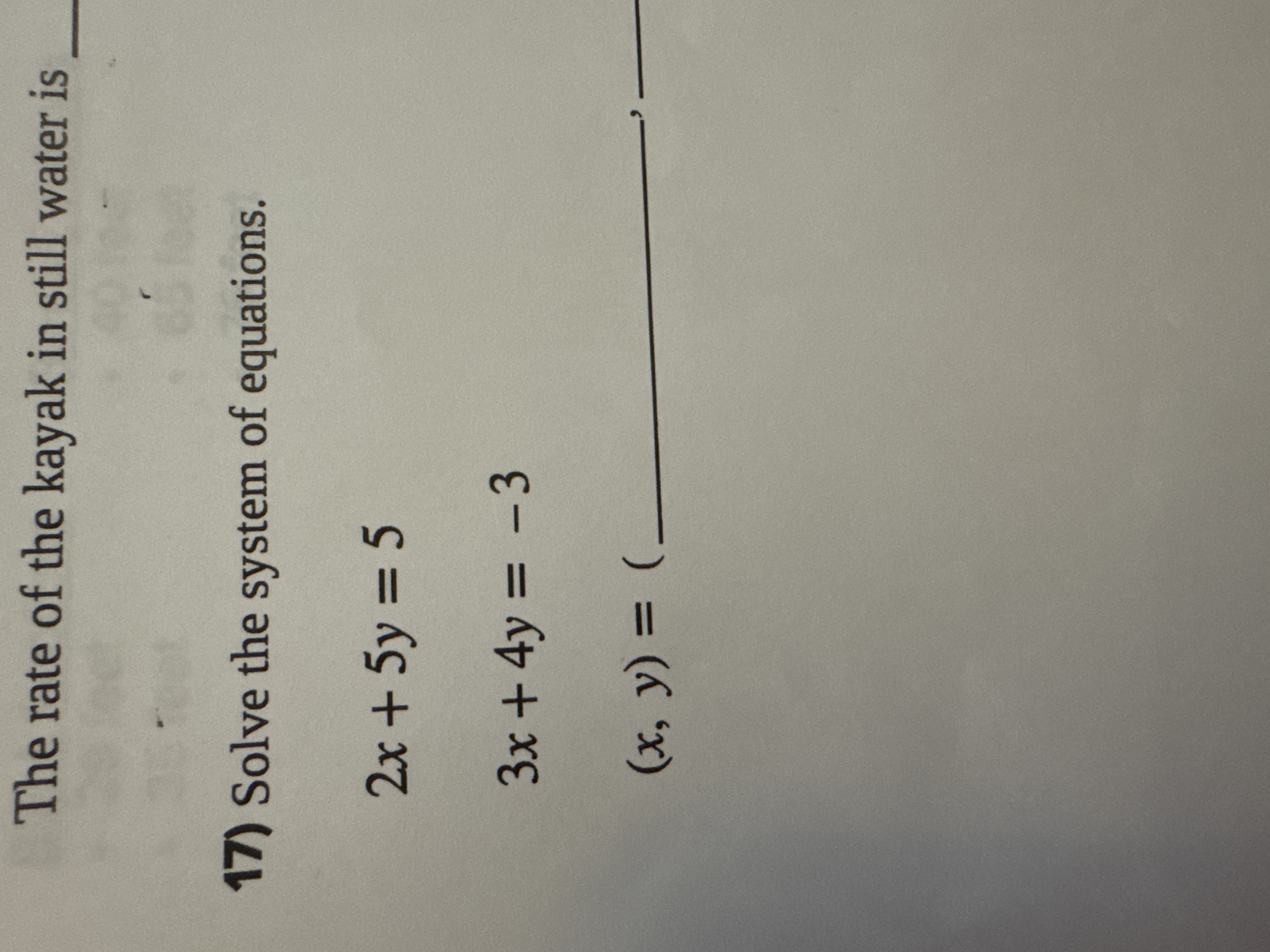
Solve the following system of equations: 2x + 5y = 5 3x + 4y = -3
Understand the Problem
The question is asking to solve a system of two linear equations with two variables (x and y). We need to find the values of x and y that satisfy both equations.
Answer
$(-5, 3)$
Answer for screen readers
$(-5, 3)$
Steps to Solve
-
Multiply the first equation by 3 and the second equation by 2 This will allow us to eliminate $x$ when we subtract the equations. $3(2x + 5y) = 3(5)$ becomes $6x + 15y = 15$ $2(3x + 4y) = 2(-3)$ becomes $6x + 8y = -6$
-
Subtract the second modified equation from the first modified equation $(6x + 15y) - (6x + 8y) = 15 - (-6)$ $6x - 6x + 15y - 8y = 15 + 6$ $7y = 21$
-
Solve for y Divide both sides of the equation by 7. $y = \frac{21}{7} = 3$
-
Substitute the value of y into one of the original equations Let's use the first equation: $2x + 5y = 5$ $2x + 5(3) = 5$ $2x + 15 = 5$
-
Solve for x Subtract 15 from both sides. $2x = 5 - 15$ $2x = -10$ Divide both sides by 2. $x = \frac{-10}{2} = -5$
-
Write the solution as an ordered pair (x, y) $(x, y) = (-5, 3)$
$(-5, 3)$
More Information
The solution to the system of equations is $x = -5$ and $y = 3$. This means that the point $(-5, 3)$ is the intersection of the two lines represented by the given equations.
Tips
A common mistake is to make errors in arithmetic when multiplying or subtracting the equations. Pay close attention to signs, especially when subtracting negative numbers. Another common mistake is to substitute the value of y back into the wrong equation or solve equation incorrectly.
AI-generated content may contain errors. Please verify critical information