Solve for g: 4 - (1/12)g - 2 = (3/2)g + 1 - (5/6)g.
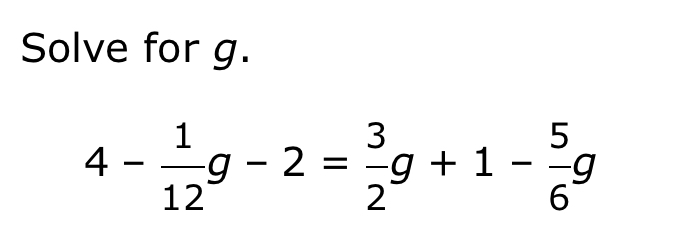
Understand the Problem
The question is asking us to solve a mathematical equation for the variable g. To do this, we will isolate g on one side of the equation by performing algebraic operations such as combining like terms and simplifying.
Answer
The value of $g$ is $g = \frac{4}{3}$.
Answer for screen readers
The solution for $g$ is:
$$ g = \frac{4}{3} $$
Steps to Solve
- Simplify both sides of the equation
Start with the original equation:
$$ 4 - \frac{1}{12}g - 2 = \frac{3}{2}g + 1 - \frac{5}{6}g $$
On the left side, simplify:
$$ 4 - 2 = 2 $$
So it becomes:
$$ 2 - \frac{1}{12}g = \frac{3}{2}g + 1 - \frac{5}{6}g $$
Next, simplify the right side by combining like terms:
Combine $\frac{3}{2}g$ and $-\frac{5}{6}g$.
Convert $\frac{3}{2}g$ to sixths:
$$ \frac{3}{2}g = \frac{9}{6}g $$
Thus, we have:
$$ \frac{9}{6}g - \frac{5}{6}g = \frac{4}{6}g = \frac{2}{3}g $$
So we update the equation to:
$$ 2 - \frac{1}{12}g = \frac{2}{3}g + 1 $$
- Isolate g on one side
Focus on isolating $g$. Start by moving the terms with $g$ to one side and constant terms to the other side.
Subtract $1$ from both sides:
$$ 2 - 1 - \frac{1}{12}g = \frac{2}{3}g $$
This simplifies to:
$$ 1 - \frac{1}{12}g = \frac{2}{3}g $$
Now, add $\frac{1}{12}g$ to both sides:
$$ 1 = \frac{2}{3}g + \frac{1}{12}g $$
- Combine g terms on the right side
To combine the $g$ terms, we need a common denominator. The least common multiple of $3$ and $12$ is $12$.
Convert $\frac{2}{3}g$ to twelfths:
$$ \frac{2}{3}g = \frac{8}{12}g $$
Now we have:
$$ 1 = \frac{8}{12}g + \frac{1}{12}g $$
This simplifies to:
$$ 1 = \frac{9}{12}g $$
- Solve for g
To isolate $g$, multiply both sides by the reciprocal of $\frac{9}{12}$, which is $\frac{12}{9}$:
$$ g = 1 \times \frac{12}{9} $$
$$ g = \frac{12}{9} $$
Now simplify this fraction:
$$ g = \frac{4}{3} $$
The solution for $g$ is:
$$ g = \frac{4}{3} $$
More Information
This fraction represents a number slightly greater than 1. It can be interpreted as an improper fraction which can also be expressed as a mixed number: $1 \frac{1}{3}$.
Tips
- Incorrectly combining terms: Ensure you get the common denominator right when combining coefficients of g.
- Sign errors: Pay careful attention to signs when moving terms from one side of the equation to the other.
AI-generated content may contain errors. Please verify critical information