Solve for f. 5 - 2/5 f + 3/2 f = f - 1/2 f + 4
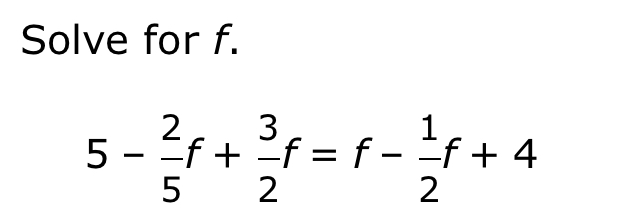
Understand the Problem
The question is asking to solve the equation for the variable f, which involves rearranging and simplifying the given equation with fractions.
Answer
$$ f = -\frac{5}{3} $$
Answer for screen readers
The solution for ( f ) is
$$ f = -\frac{5}{3} $$
Steps to Solve
- Combine like terms on the left side
Start with the equation:
$$ 5 - \frac{2}{5}f + \frac{3}{2}f = f - \frac{1}{2}f + 4 $$
Combine the terms with $f$ on the left side:
$$ -\frac{2}{5}f + \frac{3}{2}f = \left(\frac{3}{2} - \frac{2}{5}\right) f $$
To combine the fractions, find a common denominator (which is 10 in this case):
$$ \frac{3}{2} = \frac{15}{10} \quad \text{and} \quad -\frac{2}{5} = -\frac{4}{10} $$
So,
$$ \frac{15}{10} - \frac{4}{10} = \frac{11}{10} $$
The left side now becomes:
$$ 5 + \frac{11}{10} f = f - \frac{1}{2} f + 4 $$
- Combine like terms on the right side
Now, simplify the right side by combining $f$ terms:
$$ f - \frac{1}{2}f = \frac{1}{2}f $$
So the equation now reads:
$$ 5 + \frac{11}{10} f = \frac{1}{2}f + 4 $$
- Isolate the variable f
Rearrange the equation to move all $f$ terms to one side and constant terms to the other:
$$ 5 - 4 = \frac{1}{2}f - \frac{11}{10}f $$
This simplifies to:
$$ 1 = -\left(\frac{11}{10} - \frac{5}{10}\right)f $$
Where $\frac{1}{2}f = \frac{5}{10}f$.
So now:
$$ 1 = -\frac{6}{10} f $$
- Solve for f
Multiply both sides by $-\frac{10}{6}$ to isolate $f$:
$$ f = -10 \cdot \frac{1}{6} = -\frac{10}{6} $$
This simplifies to:
$$ f = -\frac{5}{3} $$
The solution for ( f ) is
$$ f = -\frac{5}{3} $$
More Information
This equation illustrates the process of combining like terms and isolating the variable. Solving equations with fractions often requires finding a common denominator, which is an important algebraic skill.
Tips
- Failing to find a common denominator when combining fractions.
- Incorrectly moving $f$ terms to one side or miscalculating during isolation steps.
- Forgetting to change the sign when multiplying or dividing by a negative number.
AI-generated content may contain errors. Please verify critical information