∫ (sin x) / (1 + cos² x) dx from b to 1/2
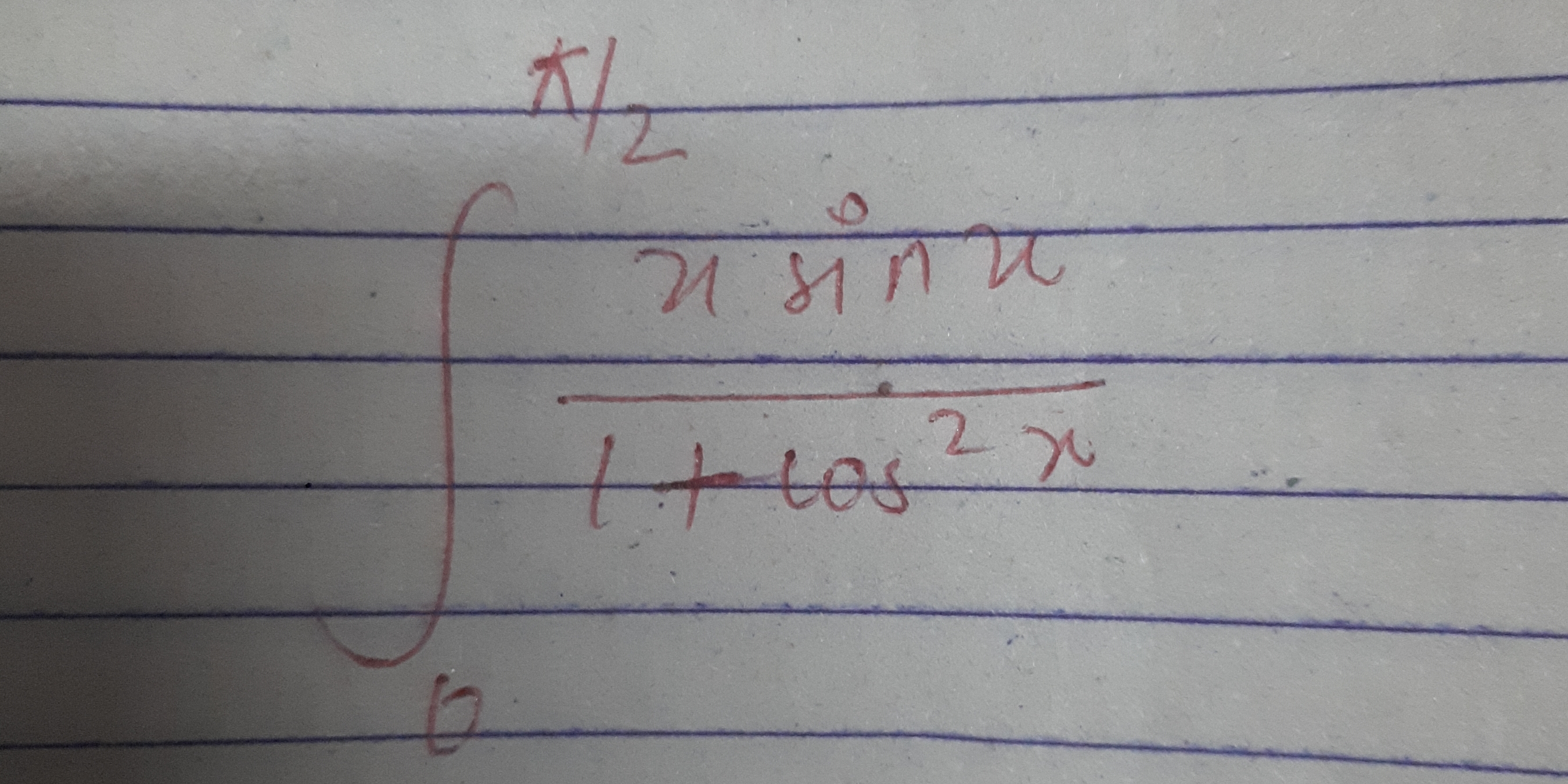
Understand the Problem
คำถามกำลังขอให้ทำการคำนวณอินทิกรัลที่มีรูปแบบซับซ้อนซึ่งเกี่ยวข้องกับฟังก์ชันตรีโกณมิติ โดยมีช่วงการอินทิเกรตจาก b ถึง rac{ rac{1}{2}}{1+ ext{cos}^2 x}
Answer
$$ \arctan(\cos b) - \frac{\pi}{3} $$
Answer for screen readers
The final answer is
$$ \arctan(\cos b) - \frac{\pi}{3} $$
Steps to Solve
- Set up the integral The integral we want to compute is
$$ \int_b^{\frac{1}{2}} \frac{\sin x}{1 + \cos^2 x} , dx $$
- Substitution
We use the substitution $u = \cos x$, which implies that $du = -\sin x , dx$. The limits of integration change accordingly:
- When $x = b$, $u = \cos b$
- When $x = \frac{1}{2}$, $u = \cos\left(\frac{1}{2}\right) = \frac{\sqrt{3}}{2}$
Thus, the integral becomes
$$ -\int_{\cos b}^{\frac{\sqrt{3}}{2}} \frac{1}{1 + u^2} , du $$
- Evaluate the integral The integral of $\frac{1}{1 + u^2}$ is
$$ \arctan u $$
Thus, we have:
$$ -\left[\arctan u\right]_{\cos b}^{\frac{\sqrt{3}}{2}} = -\left(\arctan\left(\frac{\sqrt{3}}{2}\right) - \arctan(\cos b)\right) $$
- Find the arctangent values Now we can compute the values:
$$ \arctan\left(\frac{\sqrt{3}}{2}\right) \text{ is a known value, and it simplifies to } \frac{\pi}{3}. $$
Therefore, we get:
$$ -\left(\frac{\pi}{3} - \arctan(\cos b)\right) = \arctan(\cos b) - \frac{\pi}{3} $$
The final answer is
$$ \arctan(\cos b) - \frac{\pi}{3} $$
More Information
The integral involved the use of substitution to simplify the expression. The arctangent function is commonly used in integrals involving rational functions of trigonometric identities. Knowing the values of certain trigonometric functions can simplify calculations.
Tips
- Forgotten negative sign from substitution: When using $u = \cos x$, remember to include the negative sign when changing the limits of integration.
- Miscalculating arctangent: Be cautious with values of arctangent and ensure you remember exact values for angles like $\frac{\pi}{3}$.
AI-generated content may contain errors. Please verify critical information