Simplify $-z^2(2z^4 + 10z^2 - 16)$
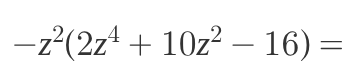
Understand the Problem
The question requires simplification of the given algebraic expression:
$\qquad -z^2(2z^4 + 10z^2 - 16)$
This involves expanding the expression by distributing $-z^2$ across the terms inside the parenthesis and simplifying the result.
Answer
$-2z^6 - 10z^4 + 16z^2$
Answer for screen readers
$-2z^6 - 10z^4 + 16z^2$
Steps to Solve
- Distribute $-z^2$ to each term inside the parenthesis
Multiply $-z^2$ by each term inside the parenthesis: $2z^4$, $10z^2$, and $-16$.
- Multiply $-z^2$ by $2z^4$
$-z^2 \cdot 2z^4 = -2z^{2+4} = -2z^6$
- Multiply $-z^2$ by $10z^2$
$-z^2 \cdot 10z^2 = -10z^{2+2} = -10z^4$
- Multiply $-z^2$ by $-16$
$-z^2 \cdot -16 = 16z^2$
- Combine the results
Combine the results from steps 2, 3, and 4 to get the simplified expression: $-2z^6 - 10z^4 + 16z^2$
$-2z^6 - 10z^4 + 16z^2$
More Information
The expression is simplified by applying the distributive property and combining like terms.
Tips
A common mistake is not correctly applying the negative sign when distributing $-z^2$ across the terms in the parenthesis. Also, mistakes can be made when adding the exponents of $z$ during multiplication. To avoid these mistakes, pay close attention to signs and remember the exponent rule $z^a \cdot z^b = z^{a+b}$.
AI-generated content may contain errors. Please verify critical information