Simplify: (x^4)^-3 * 2x^-1
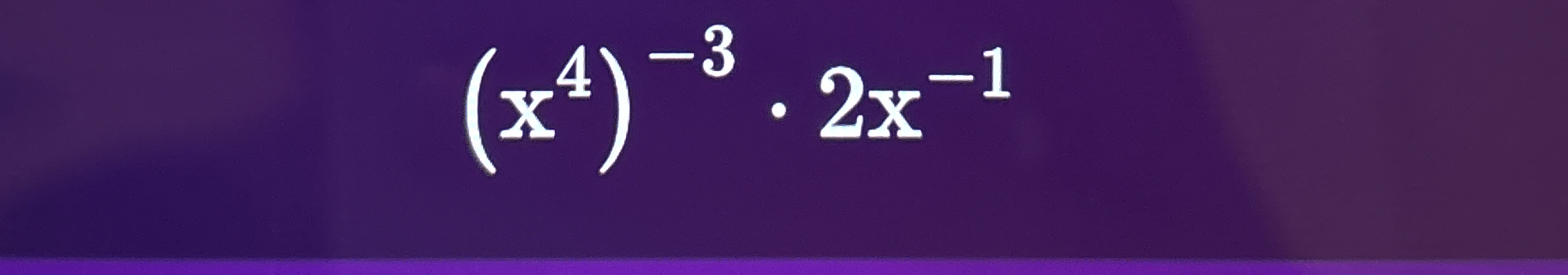
Understand the Problem
The question requires simplifying an expression with exponents. We need to apply rules of exponents such as the power of a power rule and the product of powers rule to simplify the given expression.
Answer
$\frac{2}{x^{13}}$
Answer for screen readers
$\frac{2}{x^{13}}$
Steps to Solve
-
Apply the power of a power rule Apply the power of a power rule which states that $(a^m)^n = a^{m \cdot n}$ to simplify $(x^4)^{-3}$ $(x^4)^{-3} = x^{4 \cdot (-3)} = x^{-12}$
-
Rewrite the original expression Substitute $x^{-12}$ back into the original expression to get: $x^{-12} \cdot 2x^{-1}$
-
Apply the product of powers rule Apply the product of powers rule which states that $a^m \cdot a^n = a^{m+n}$ to simplify $x^{-12} \cdot x^{-1}$ $x^{-12} \cdot x^{-1} = x^{-12 + (-1)} = x^{-13}$
-
Simplify the expression Rewrite the complete expression: $2x^{-13} = \frac{2}{x^{13}}$
$\frac{2}{x^{13}}$
More Information
The expression $(x^4)^{-3} \cdot 2x^{-1}$ simplifies to $\frac{2}{x^{13}}$. This involves using the power of a power rule and the product of powers rule.
Tips
A common mistake is to incorrectly apply the power of a power rule or the product of powers rule. For example, students might add the exponents when they should multiply them in the power of a power rule, or multiply the bases when applying the product of powers rule. Another common mistake is not handling the negative exponents correctly, resulting in incorrect placement of the variable in the numerator or denominator.
AI-generated content may contain errors. Please verify critical information