Evaluate the integral: ∫ (x+8) / √(9-x^2) dx
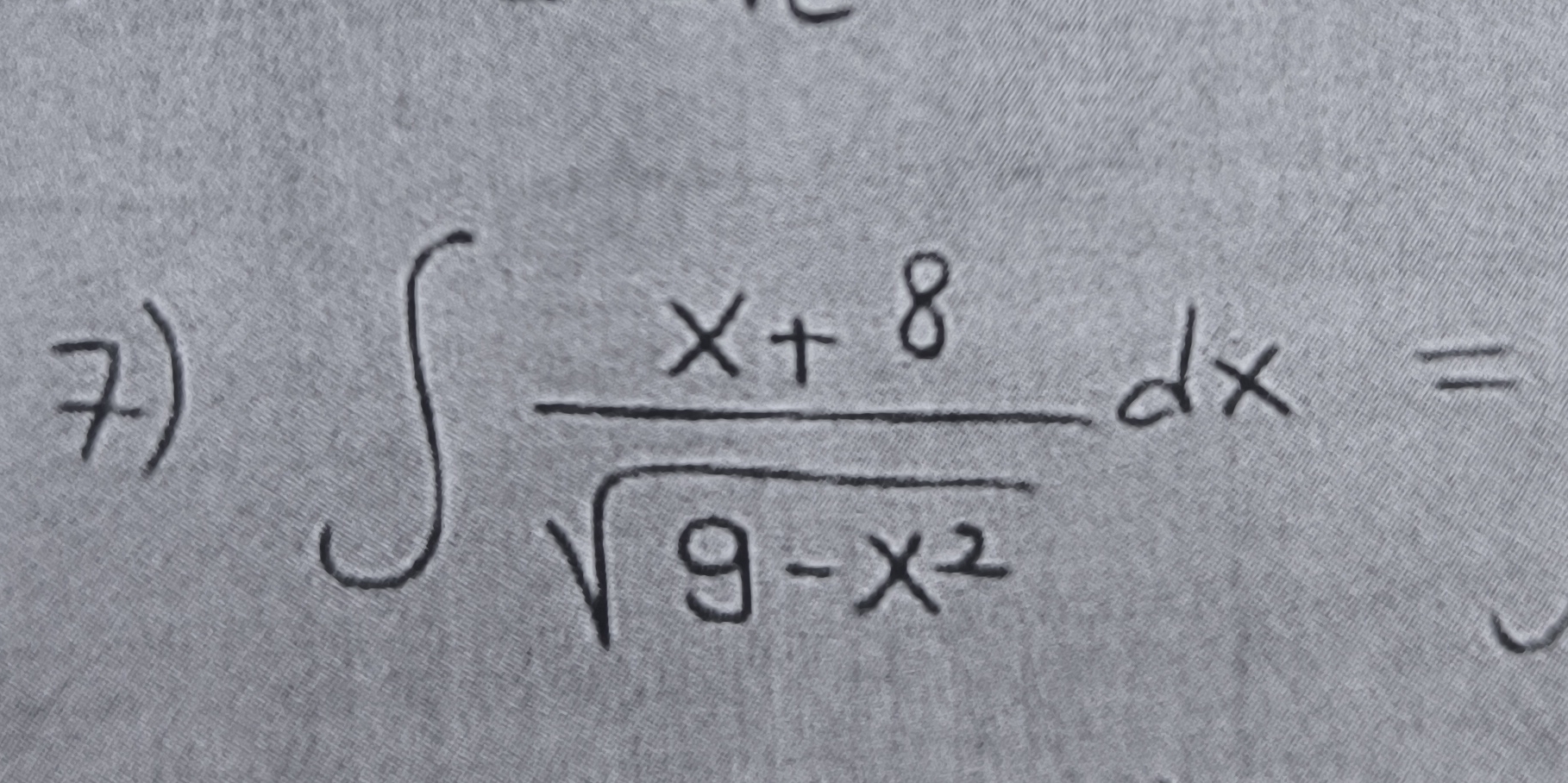
Understand the Problem
The question asks to evaluate the integral of a rational function where the numerator is a linear function (x+8) and the denominator involves the square root of a quadratic expression (9-x^2). The integral can be split up into two separate integrals, one involving x and the other a constant, both divided by the same square root term. These resulting integrals require different substitution techniques to solve.
Answer
$$ -\sqrt{9-x^2} + 8\arcsin\left(\frac{x}{3}\right) + C $$
Answer for screen readers
$$ -\sqrt{9-x^2} + 8\arcsin\left(\frac{x}{3}\right) + C $$
Steps to Solve
-
Split the integral into two separate integrals Separate the original integral into two integrals, one with $x$ in the numerator and the other with the constant $8$ in the numerator. $$ \int \frac{x+8}{\sqrt{9-x^2}} dx = \int \frac{x}{\sqrt{9-x^2}} dx + \int \frac{8}{\sqrt{9-x^2}} dx $$
-
Solve the first integral using u-substitution Let $u = 9 - x^2$, then $du = -2x , dx$. So, $x , dx = -\frac{1}{2} du$. Substitute these into the first integral: $$ \int \frac{x}{\sqrt{9-x^2}} dx = \int \frac{-\frac{1}{2}}{\sqrt{u}} du = -\frac{1}{2} \int u^{-1/2} du $$ Now integrate with respect to $u$: $$ -\frac{1}{2} \int u^{-1/2} du = -\frac{1}{2} \cdot \frac{u^{1/2}}{1/2} + C_1 = -u^{1/2} + C_1 $$ Substitute $u = 9 - x^2$ back into the expression: $$ -u^{1/2} + C_1 = -\sqrt{9-x^2} + C_1 $$
-
Solve the second integral using trigonometric substitution The second integral is $\int \frac{8}{\sqrt{9-x^2}} dx$. We can rewrite this as $8 \int \frac{1}{\sqrt{3^2 - x^2}} dx$. Perform the substitution $x = 3\sin(\theta)$, where $dx = 3\cos(\theta) , d\theta$. Then $\sqrt{9-x^2} = \sqrt{9 - 9\sin^2(\theta)} = \sqrt{9(1-\sin^2(\theta))} = \sqrt{9\cos^2(\theta)} = 3\cos(\theta)$. Thus, $$ 8 \int \frac{1}{\sqrt{9-x^2}} dx = 8 \int \frac{3\cos(\theta)}{3\cos(\theta)} d\theta = 8 \int 1 , d\theta = 8\theta + C_2 $$ Since $x = 3\sin(\theta)$, we have $\sin(\theta) = \frac{x}{3}$, so $\theta = \arcsin\left(\frac{x}{3}\right)$. Substitute this back into the expression: $$ 8\theta + C_2 = 8\arcsin\left(\frac{x}{3}\right) + C_2 $$
-
Combine the results Add the results of the two integrals: $$ \int \frac{x+8}{\sqrt{9-x^2}} dx = -\sqrt{9-x^2} + 8\arcsin\left(\frac{x}{3}\right) + C $$ where $C = C_1 + C_2$ is the constant of integration.
$$ -\sqrt{9-x^2} + 8\arcsin\left(\frac{x}{3}\right) + C $$
More Information
The integral combines a standard u-substitution with a trigonometric substitution, showcasing different techniques for handling integrals involving square roots of quadratic expressions.
Tips
A common mistake is forgetting the constant of integration, $C$. Also, errors can occur during the u-substitution process (forgetting the negative sign) or during the trigonometric substitution (incorrectly finding $dx$ or simplifying the square root).
AI-generated content may contain errors. Please verify critical information