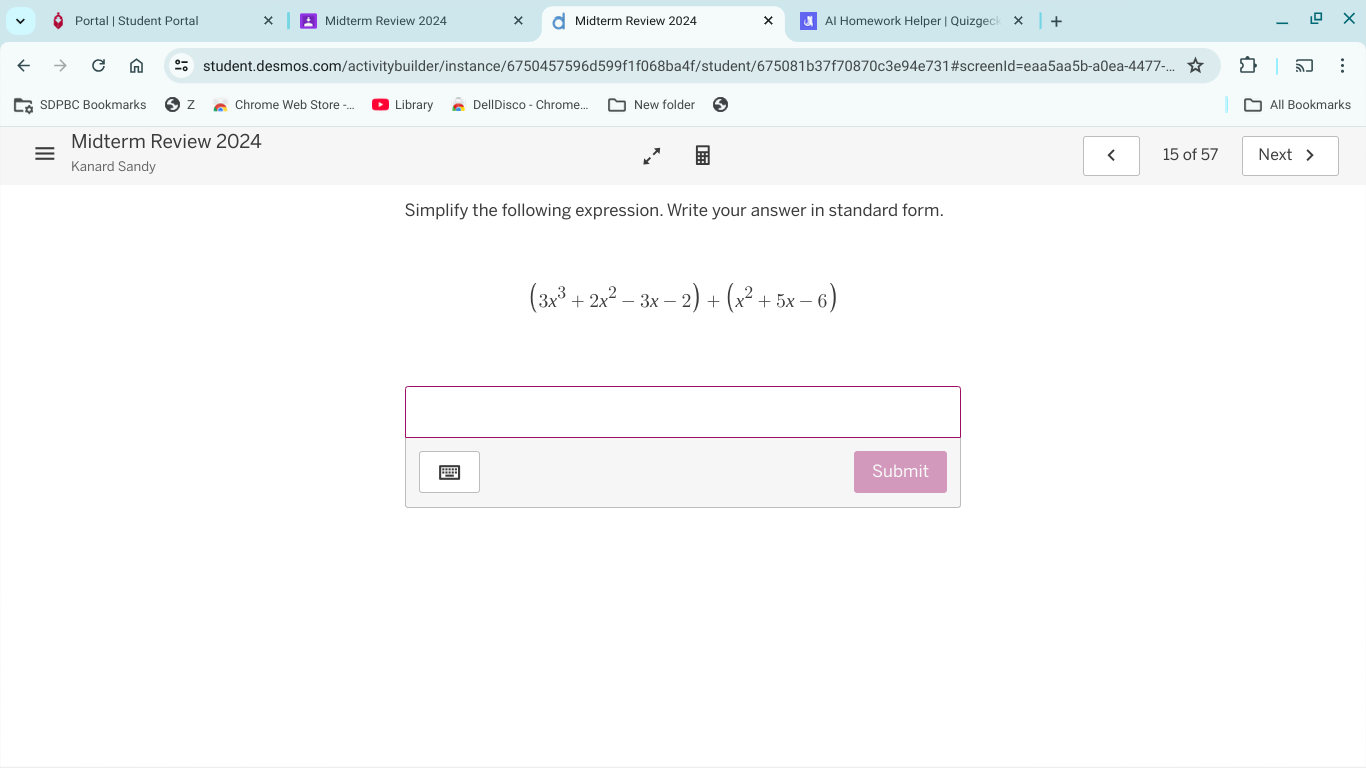
Simplify the following expression. Write your answer in standard form: (3x^3 + 2x^2 - 3x - 2) + (x^2 + 5x - 6)
Understand the Problem
The question is asking to simplify the given polynomial expression and write the result in standard form. This involves combining like terms and arranging them according to the degree of the terms.
Answer
The final simplified expression is: $$3x^3 + 3x^2 + 2x - 8$$
Answer for screen readers
The simplified expression in standard form is: $$3x^3 + 3x^2 + 2x - 8$$
Steps to Solve
-
Write down the expression First, we'll combine all parts of the given polynomial expression: $$(3x^3 + 2x^2 - 3x - 2) + (x^2 + 5x - 6)$$
-
Remove the parentheses Since there is no negative sign before the second parenthesis, we can simply write it out together: $$3x^3 + 2x^2 - 3x - 2 + x^2 + 5x - 6$$
-
Combine like terms We identify terms with the same degree (like terms) and combine them:
- For $x^3$ terms: $3x^3$
- For $x^2$ terms: $2x^2 + x^2 = 3x^2$
- For $x$ terms: $-3x + 5x = 2x$
- For constant terms: $-2 - 6 = -8$
-
Rewrite the simplified expression Putting all the combined terms together, we get: $$3x^3 + 3x^2 + 2x - 8$$
The simplified expression in standard form is: $$3x^3 + 3x^2 + 2x - 8$$
More Information
In polynomial expressions, standard form means writing the terms in order of decreasing degree. This ensures clarity when dealing with functions or algebraic manipulations.
Tips
- Failing to combine all like terms correctly can result in missing or incorrect coefficients.
- Forgetting to apply the signs accurately when combining constants.
AI-generated content may contain errors. Please verify critical information