Simplify the following expression: \(\frac{3x^5}{(-3x^3)^2}\)
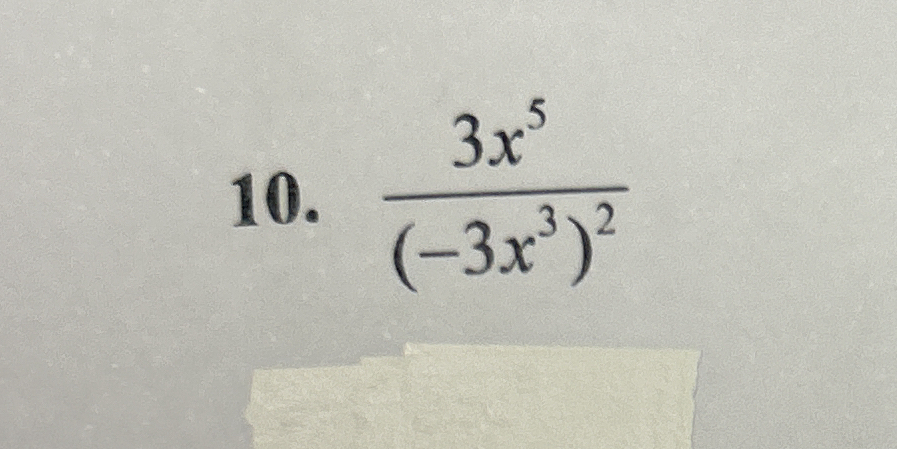
Understand the Problem
The question requires simplifying an algebraic expression. The expression involves a fraction with terms containing exponents. The numerator is (3x^5), and the denominator is ((-3x^3)^2).
Answer
$\frac{1}{3x}$
Answer for screen readers
$\frac{1}{3x}$
Steps to Solve
- Simplify the denominator Apply the power rule to simplify the denominator ((-3x^3)^2). $$ (-3x^3)^2 = (-3)^2 \cdot (x^3)^2 = 9x^6 $$
- Rewrite the expression Substitute the simplified denominator back into the original expression: $$ \frac{3x^5}{9x^6} $$
- Simplify the fraction Divide both the numerator and the denominator by their greatest common factor. $$ \frac{3x^5}{9x^6} = \frac{3}{9} \cdot \frac{x^5}{x^6} = \frac{1}{3} \cdot x^{5-6} = \frac{1}{3} \cdot x^{-1} $$
- Rewrite with a positive exponent Rewrite $x^{-1}$ as $\frac{1}{x}$: $$ \frac{1}{3} \cdot x^{-1} = \frac{1}{3} \cdot \frac{1}{x} = \frac{1}{3x} $$
$\frac{1}{3x}$
More Information
The simplified form of the given expression is $\frac{1}{3x}$.
Tips
- Forgetting to apply the exponent to both the coefficient and the variable in the denominator. For example, incorrectly calculating $(-3x^3)^2$ as $-9x^6$ or $-3x^6$.
- Incorrectly simplifying the exponents when dividing. Remember to subtract the exponent in the denominator from the exponent in the numerator.
- Not simplifying the fraction $\frac{3}{9}$ to $\frac{1}{3}$.
AI-generated content may contain errors. Please verify critical information