Simplify the following expression: (a^-4 * b^2) / (b * a^2 * a^2 * b^-4) ^ -3
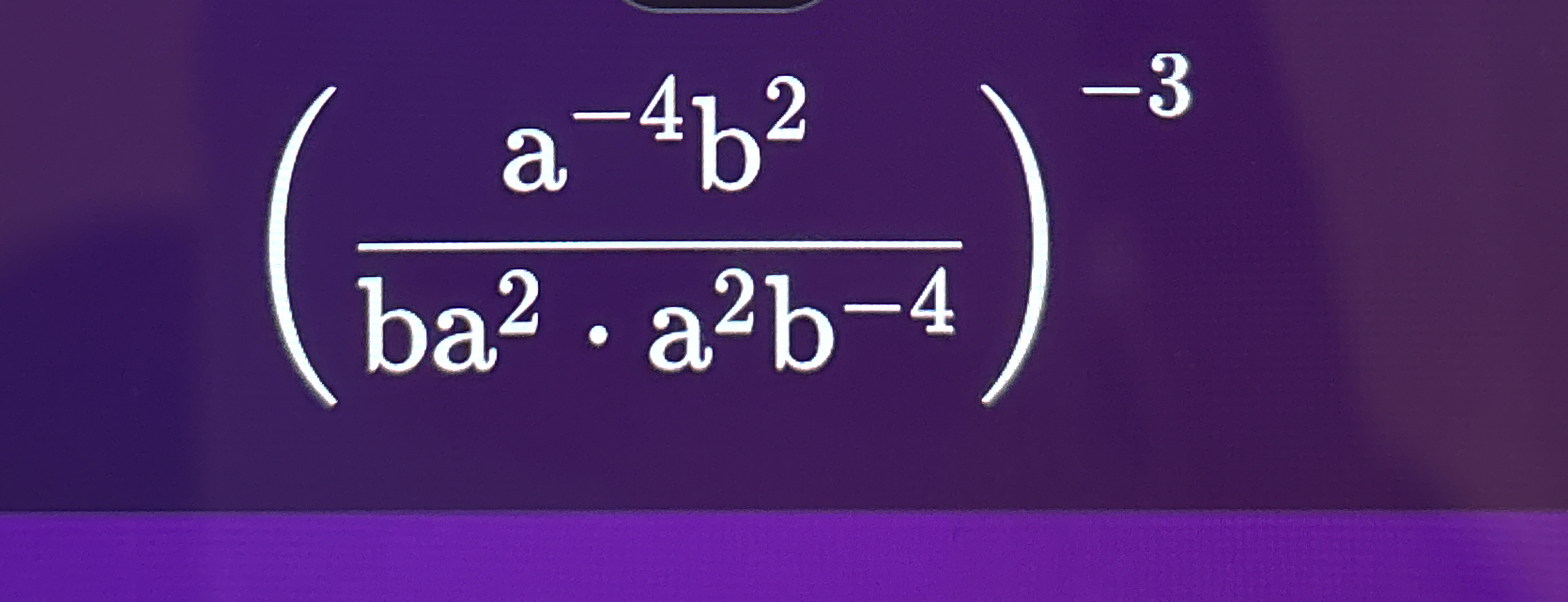
Understand the Problem
The question requires simplifying an algebraic expression with exponents. We will simplify the expression inside the parenthesis first using exponent rules, and then apply the outer exponent.
Answer
$\frac{a^{24}}{b^{15}}$
Answer for screen readers
$\frac{a^{24}}{b^{15}}$
Steps to Solve
-
Simplify the denominator Combine like terms in the denominator by adding exponents with the same base. $ba^2 \cdot a^2b^{-4} = a^{2+2}b^{1+(-4)} = a^4b^{-3}$
-
Rewrite the expression Substitute the simplified denominator back into the original expression: $\left(\frac{a^{-4}b^{2}}{a^4b^{-3}}\right)^{-3}$
-
Simplify inside the parenthesis Divide terms with the same base by subtracting the exponents. $\frac{a^{-4}}{a^4} = a^{-4-4} = a^{-8}$ $\frac{b^2}{b^{-3}} = b^{2-(-3)} = b^{2+3} = b^5$ So, we have: $(a^{-8}b^{5})^{-3}$
-
Apply the outer exponent Apply the outer exponent of $-3$ to both $a^{-8}$ and $b^5$. $(a^{-8})^{-3} = a^{(-8)(-3)} = a^{24}$ $(b^{5})^{-3} = b^{(5)(-3)} = b^{-15}$ So we have: $a^{24}b^{-15}$
-
Rewrite with positive exponents Rewrite the expression such that all exponents are positive. $a^{24}b^{-15} = \frac{a^{24}}{b^{15}}$
$\frac{a^{24}}{b^{15}}$
More Information
The simplified form of the given expression is $\frac{a^{24}}{b^{15}}$. In simplifying expressions with exponents, it's crucial to remember the rules for multiplying and dividing terms with the same base, as well as how to handle negative exponents.
Tips
A common mistake is incorrectly applying the exponent rules, especially when dealing with negative exponents. For example, when dividing terms with the same base, students might add the exponents instead of subtracting them. Another mistake is not distributing the outer exponent correctly to all terms inside the parenthesis.
AI-generated content may contain errors. Please verify critical information