Simplify the following expression: ((-3x)^2 * (-5y)^3) / (25 * (-x)^2 * (-y))
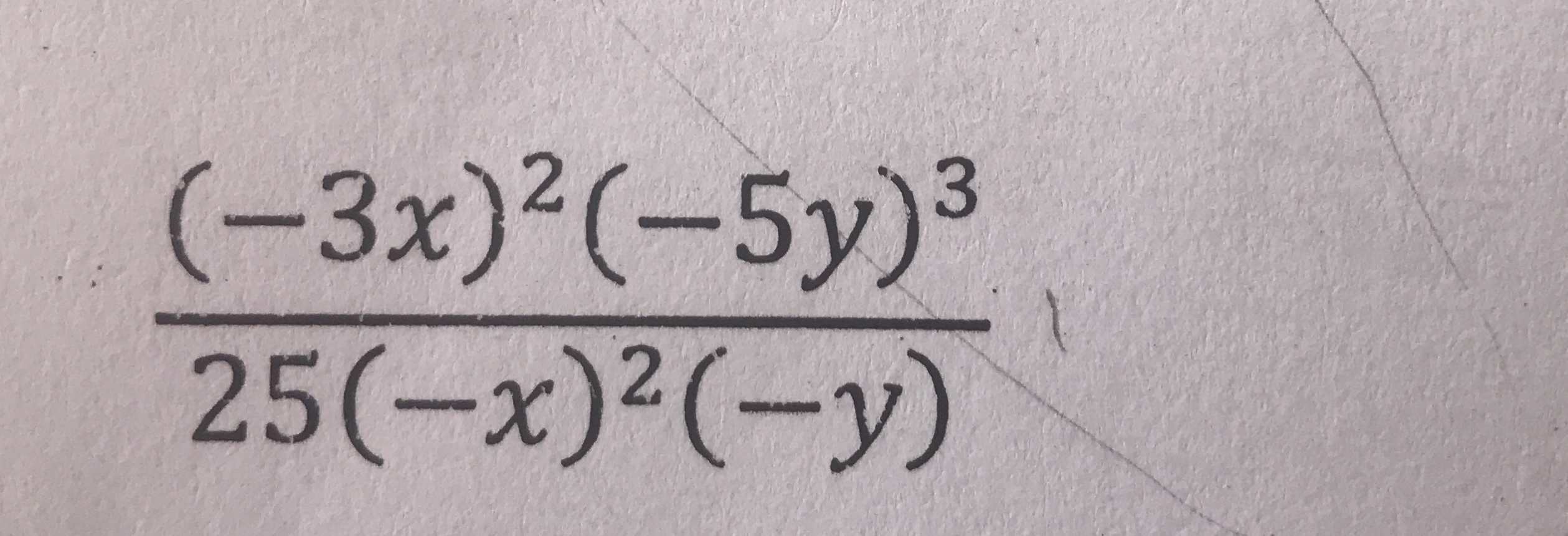
Understand the Problem
The question requires simplifying the given expression with exponents and variables. We need to apply the rules of exponents and simplify the numerical coefficients and variable terms.
Answer
$45y^2$
Answer for screen readers
$45y^2$
Steps to Solve
-
Expand the terms in the numerator. Expand $(-3x)^2$ to get $(-3)^2 \cdot x^2 = 9x^2$. Expand $(-5y)^3$ to get $(-5)^3 \cdot y^3 = -125y^3$. So the numerator becomes $9x^2 \cdot (-125y^3) = -1125x^2y^3$.
-
Expand the terms in the denominator. Expand $(-x)^2$ to get $x^2$. Expand $(-y)$ to get $-y$. So the denominator becomes $25 \cdot x^2 \cdot (-y) = -25x^2y$.
-
Write the simplified expression. The expression becomes $\frac{-1125x^2y^3}{-25x^2y}$.
-
Simplify the numerical coefficients. Divide $-1125$ by $-25$ to get $\frac{-1125}{-25} = 45$.
-
Simplify the variable terms. Divide $x^2$ by $x^2$ to get $\frac{x^2}{x^2} = 1$. Divide $y^3$ by $y$ to get $\frac{y^3}{y} = y^{3-1} = y^2$.
-
Combine the simplified terms. The simplified expression is $45 \cdot 1 \cdot y^2 = 45y^2$.
$45y^2$
More Information
The expression simplifies to $45y^2$. This indicates that the original expression is equivalent to a quadratic function in terms of $y$, where the coefficient is 45.
Tips
A common mistake when simplifying expressions with exponents is incorrectly applying the power to the coefficient and variable. For example, $(-3x)^2$ might be incorrectly simplified as $-9x^2$ instead of $9x^2$. Another mistake is forgetting to apply the exponent to both the coefficient and the variable inside the parentheses. Also, mistakes are made when dividing variables with exponents, forgetting that you need to subtract the exponents. Careless sign errors are also easy to make.
AI-generated content may contain errors. Please verify critical information