Simplify the expression: $(x - 1)^2 - (x - 5)(2x + 3)$
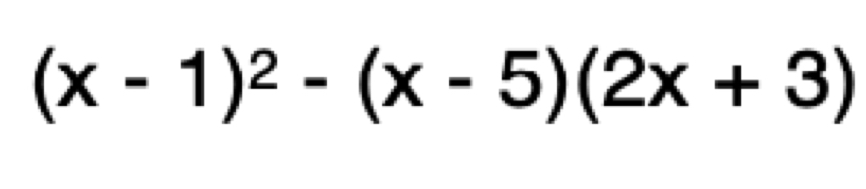
Understand the Problem
The question requires the simplification of the algebraic expression. This involves expanding the squared term and the product of binomials, and then combining like terms to obtain the simplified expression.
Answer
$-x^2 + 5x + 16$
Answer for screen readers
$-x^2 + 5x + 16$
Steps to Solve
- Expanding $(x - 1)^2$
We expand the first term, which is a binomial squared:
$(x - 1)^2 = (x - 1)(x - 1) = x^2 - x - x + 1 = x^2 - 2x + 1$
- Expanding $(x - 5)(2x + 3)$
Next, we expand the product of the two binomials:
$(x - 5)(2x + 3) = 2x^2 + 3x - 10x - 15 = 2x^2 - 7x - 15$
- Substituting back into the original expression
Now we substitute these expansions back into the original expression:
$(x - 1)^2 - (x - 5)(2x + 3) = (x^2 - 2x + 1) - (2x^2 - 7x - 15)$
- Distributing the negative sign
Distribute the negative sign in front of the second term:
$x^2 - 2x + 1 - 2x^2 + 7x + 15$
- Combining like terms
Combine the like terms:
$(x^2 - 2x^2) + (-2x + 7x) + (1 + 15) = -x^2 + 5x + 16$
$-x^2 + 5x + 16$
More Information
The simplified expression is a quadratic expression.
Tips
A common mistake is not distributing the negative sign correctly when subtracting the second expression. Remember to change the sign of every term inside the parentheses. Another common mistake involves errors during FOILing. Make sure each term in one parenthesis is multiplied by each term in the other parenthesis.
AI-generated content may contain errors. Please verify critical information