Simplify the expression: $\frac{(9^{-1})500}{(3^{500})^3}$
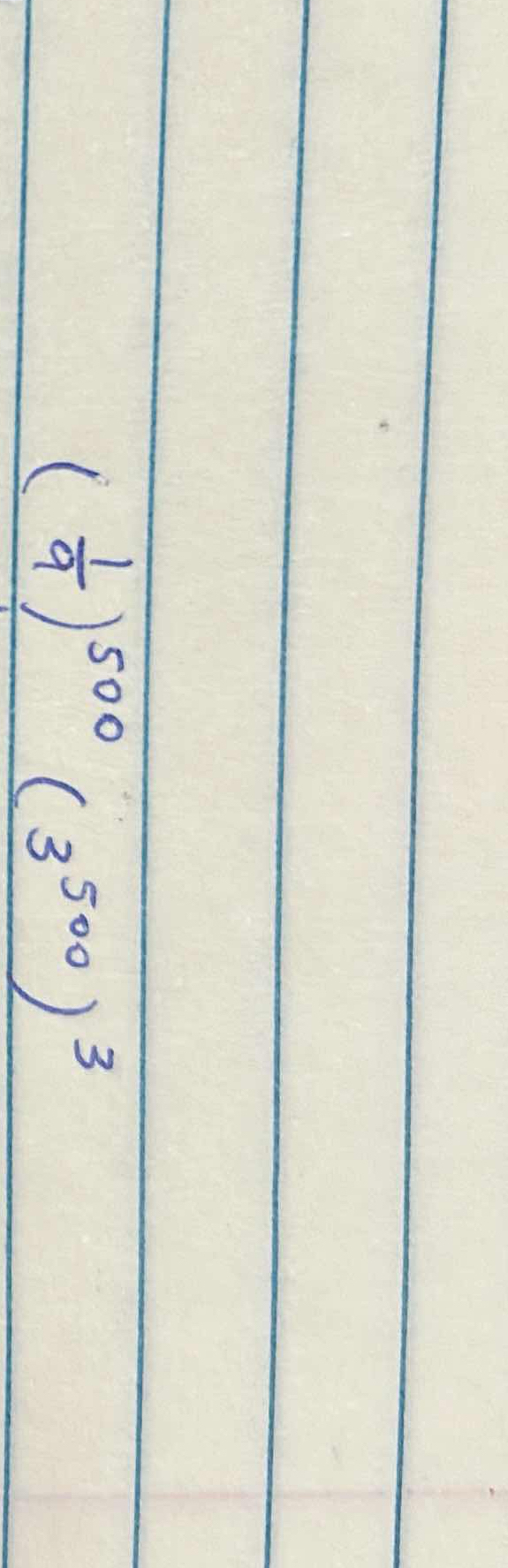
Understand the Problem
The question is asking to simplify the expression $\frac{(9^{-1})500}{(3^{500})^3}$. We will need to use the properties of exponents to simplify the expression.
Answer
$500 \cdot 3^{-1502}$
Answer for screen readers
$500 \cdot 3^{-1502}$
Steps to Solve
- Rewrite $9^{-1}$ as a power of 3
We can rewrite $9$ as $3^2$. Therefore, $9^{-1} = (3^2)^{-1}$.
- Simplify $(3^2)^{-1}$
Using the power of a power rule, $(a^m)^n = a^{mn}$, we have $(3^2)^{-1} = 3^{2*(-1)} = 3^{-2}$.
- Simplify $(3^{500})^3$
Using the power of a power rule again, $(3^{500})^3 = 3^{500*3} = 3^{1500}$.
- Rewrite the original expression
Substitute the results from steps 2 and 3 into the original expression: $\frac{(9^{-1})500}{(3^{500})^3} = \frac{3^{-2} \cdot 500}{3^{1500}}$.
- Simplify the expression
Now we have $\frac{3^{-2} \cdot 500}{3^{1500}}$. We can rewrite this as $500 \cdot \frac{3^{-2}}{3^{1500}}$. When dividing powers with the same base, we subtract the exponents. $500 \cdot \frac{3^{-2}}{3^{1500}} = 500 \cdot 3^{-2-1500} = 500 \cdot 3^{-1502}$.
- Final Answer
Therefore, the simplified expression is $500 \cdot 3^{-1502}$.
$500 \cdot 3^{-1502}$
More Information
The answer $500 \cdot 3^{-1502}$ can also be written as $\frac{500}{3^{1502}}$. $3^{1502}$ is a very large number, so leaving the answer in the form $500 \cdot 3^{-1502}$ or $\frac{500}{3^{1502}}$ is perfectly acceptable.
Tips
- Forgetting the power of a power rule: make sure to multiply the exponents when raising a power to another power.
- Incorrectly applying the quotient of powers rule: make sure to subtract the exponents correctly when dividing powers with the same base.
AI-generated content may contain errors. Please verify critical information