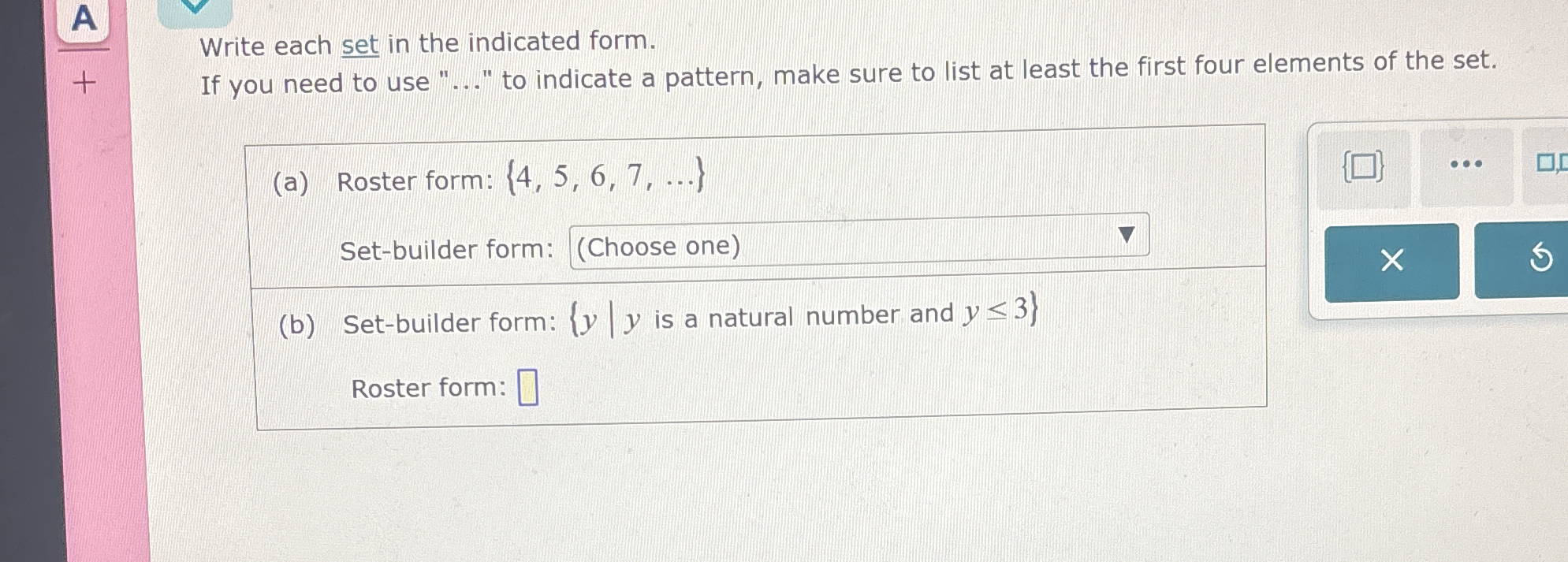
Write each set in the indicated form. If you need to use "..." to indicate a pattern, make sure to list at least the first four elements of the set. (a) Roster form: {4, 5, 6, 7, .... Write each set in the indicated form. If you need to use "..." to indicate a pattern, make sure to list at least the first four elements of the set. (a) Roster form: {4, 5, 6, 7, ...} Set-builder form: (b) Set-builder form: {y | y is a natural number and y ≤ 3} Roster form:
Understand the Problem
The question asks to convert sets between roster form and set-builder form. For part (a) the set is given in roster form, and requires choosing the correct set-builder form. Part (b) gives the set-builder form, and requires writing the roster form.
Answer
(a) $\{ x \mid x \in \mathbb{N} \text{ and } x \geq 4 \}$ (b) $\{1, 2, 3\}$
Answer for screen readers
(a) ${ x \mid x \in \mathbb{N} \text{ and } x \geq 4 }$ (b) ${1, 2, 3}$
Steps to Solve
- Part (a): Identify the pattern in the roster form
The set {4, 5, 6, 7, ...} represents all natural numbers starting from 4.
- Part (a): Choose the correct set-builder form
The correct set-builder form should describe the same set. The set-builder form is ${ x \mid x \in \mathbb{N} \text{ and } x \geq 4 }$.
- Part (b): Understand the set-builder form
The set {y | y is a natural number and y ≤ 3} describes the set of all natural numbers $y$ such that $y$ is less than or equal to 3.
- Part (b): List the elements in roster form
The natural numbers less than or equal to 3 are 1, 2, and 3. Therefore, the roster form is {1, 2, 3}.
(a) ${ x \mid x \in \mathbb{N} \text{ and } x \geq 4 }$ (b) ${1, 2, 3}$
More Information
Natural numbers are positive integers (also known as counting numbers), starting from 1 and going to infinity: 1, 2, 3, 4, ...
Tips
A common mistake in part (a) is to not realize which set builder notation accurately represents the numbers $4, 5, 6, 7, ...$.
A common mistake many people make in part (b) is including zero, but zero is not a natural number.
AI-generated content may contain errors. Please verify critical information