Simplify the expression: (4p^6 - 20p^4 + 16p) / (12p)
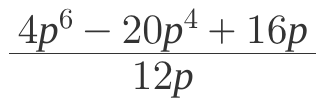
Understand the Problem
The question requires simplifying a rational expression. This involves factoring both the numerator and denominator, then canceling common factors to arrive at the simplest form. The key is to identify common factors in the numerator to facilitate simplification with the denominator.
Answer
$\frac{p^5 - 5p^3 + 4}{3}$
Answer for screen readers
$\frac{p^5 - 5p^3 + 4}{3}$
Steps to Solve
- Factor out common factors from the numerator
We can factor out $4p$ from each term in the numerator:
$$ \frac{4p^6 - 20p^4 + 16p}{12p} = \frac{4p(p^5 - 5p^3 + 4)}{12p} $$
- Simplify by canceling common factors
Now we can cancel the common factor of $4p$ from the numerator and denominator:
$$\frac{4p(p^5 - 5p^3 + 4)}{12p} = \frac{p^5 - 5p^3 + 4}{3}$$
$\frac{p^5 - 5p^3 + 4}{3}$
More Information
The simplified form of the expression is $\frac{p^5 - 5p^3 + 4}{3}$. Further factorization of the numerator is possible but not required for full simplification.
Tips
A common mistake would be incorrectly factoring out the common terms from the numerator. Always double-check by distributing the factored term back into the expression to ensure it matches the original numerator. Another mistake would be to prematurely cancel terms before factoring.
AI-generated content may contain errors. Please verify critical information