Simplify $\sqrt[3]{-81} + 4\sqrt[3]{3}$
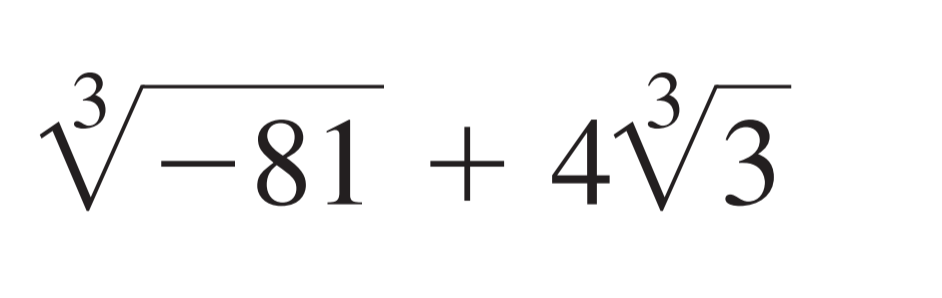
Understand the Problem
The question is asking us to simplify an expression involving cube roots. We need to simplify $\sqrt[3]{-81} + 4\sqrt[3]{3}$.
Answer
$\sqrt[3]{3}$
Answer for screen readers
$\sqrt[3]{3}$
Steps to Solve
-
Simplify $\sqrt[3]{-81}$ We can rewrite $-81$ as $-27 \cdot 3$. Then we have $$ \sqrt[3]{-81} = \sqrt[3]{-27 \cdot 3} = \sqrt[3]{-27} \cdot \sqrt[3]{3} = -3\sqrt[3]{3} $$
-
Substitute the simplified cube root into the original expression Now we substitute $-3\sqrt[3]{3}$ for $\sqrt[3]{-81}$ in the original expression: $$ \sqrt[3]{-81} + 4\sqrt[3]{3} = -3\sqrt[3]{3} + 4\sqrt[3]{3} $$
-
Combine like terms Since both terms have the same radical part, $\sqrt[3]{3}$, we can combine them like regular variables: $$ -3\sqrt[3]{3} + 4\sqrt[3]{3} = (-3 + 4)\sqrt[3]{3} = 1\sqrt[3]{3} = \sqrt[3]{3} $$
$\sqrt[3]{3}$
More Information
The simplified expression is $\sqrt[3]{3}$. This is the cube root of 3, which is an irrational number approximately equal to 1.442.
Tips
A common mistake is incorrectly simplifying $\sqrt[3]{-81}$. Remember that $\sqrt[3]{-81} = \sqrt[3]{-27 \cdot 3} = -3\sqrt[3]{3}$, not $-9\sqrt[3]{3}$ or some other incorrect simplification. Also, be careful with the negative sign. Another common mistake is forgetting to combine the coefficients correctly after simplifying the cube roots, e.g. by incorrectly adding $-3+4$.
AI-generated content may contain errors. Please verify critical information