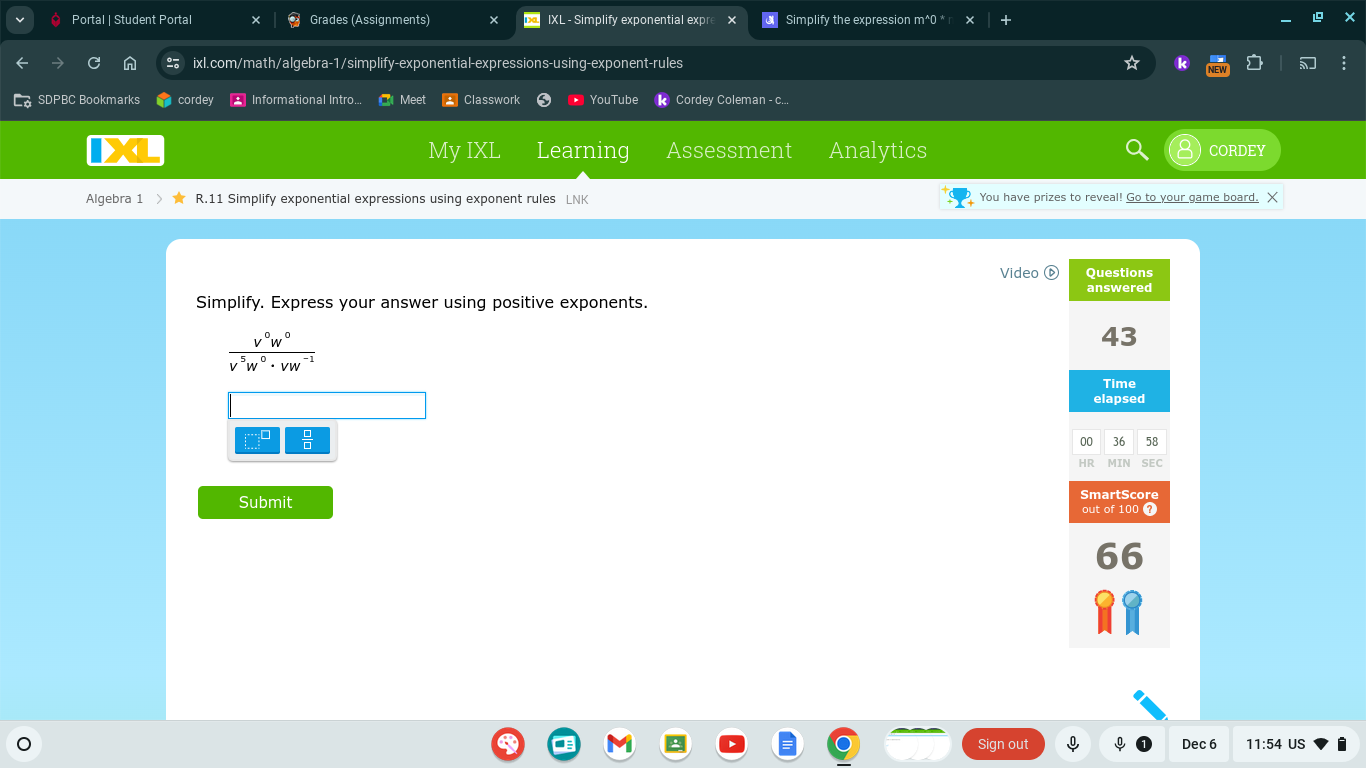
Simplify. Express your answer using positive exponents: (v^0 * w^0) / (5 * v^w * w^(-1))
Understand the Problem
The question is asking to simplify the given exponential expression and to present the answer with positive exponents. This involves applying the rules of exponents to reduce the expression to its simplest form.
Answer
The simplified expression is $$ \frac{w}{5v}. $$
Answer for screen readers
The final simplified expression is
$$ \frac{w}{5v}. $$
Steps to Solve
- Identify the Expression The given expression to simplify is
$$ \frac{v^0 w^0}{5^{w^0} \cdot vw^{-1}} $$.
-
Simplify the Numerator Recall that any non-zero number raised to the power of 0 is equal to 1. Therefore, $$ v^0 = 1 \quad \text{and} \quad w^0 = 1 $$. Thus, the numerator simplifies to $$ 1 \cdot 1 = 1. $$
-
Simplify the Denominator Now, simplify the denominator:
- We know that $w^0 = 1$, so $5^{w^0} = 5^1 = 5$.
- For $vw^{-1}$, we can rewrite it as $\frac{v}{w}$.
Thus, the denominator becomes $$ 5 \cdot vw^{-1} = 5 \cdot \frac{v}{w} = \frac{5v}{w}. $$
- Rewrite the Fraction Incorporating the simplifications made, the overall expression now looks like this:
$$ \frac{1}{\frac{5v}{w}}. $$
- Inverse the Denominator To simplify further, take the reciprocal of the denominator:
$$ 1 \cdot \frac{w}{5v} = \frac{w}{5v}. $$
The final simplified expression is
$$ \frac{w}{5v}. $$
More Information
In mathematics, simplifying expressions is important for reducing complexity and making calculations easier. The rule that any number raised to the power of 0 equals 1 is fundamental in algebra and is widely used.
Tips
- Forgetting that $a^0 = 1$ for any non-zero $a$. This is crucial for correctly simplifying expressions involving zeros in the exponent.
- Misunderstanding how to deal with negative exponents; remember that $a^{-n} = \frac{1}{a^n}$.
AI-generated content may contain errors. Please verify critical information