Simplify: (5^(x+1) - 5^(2+x)) / (5^(x-1))
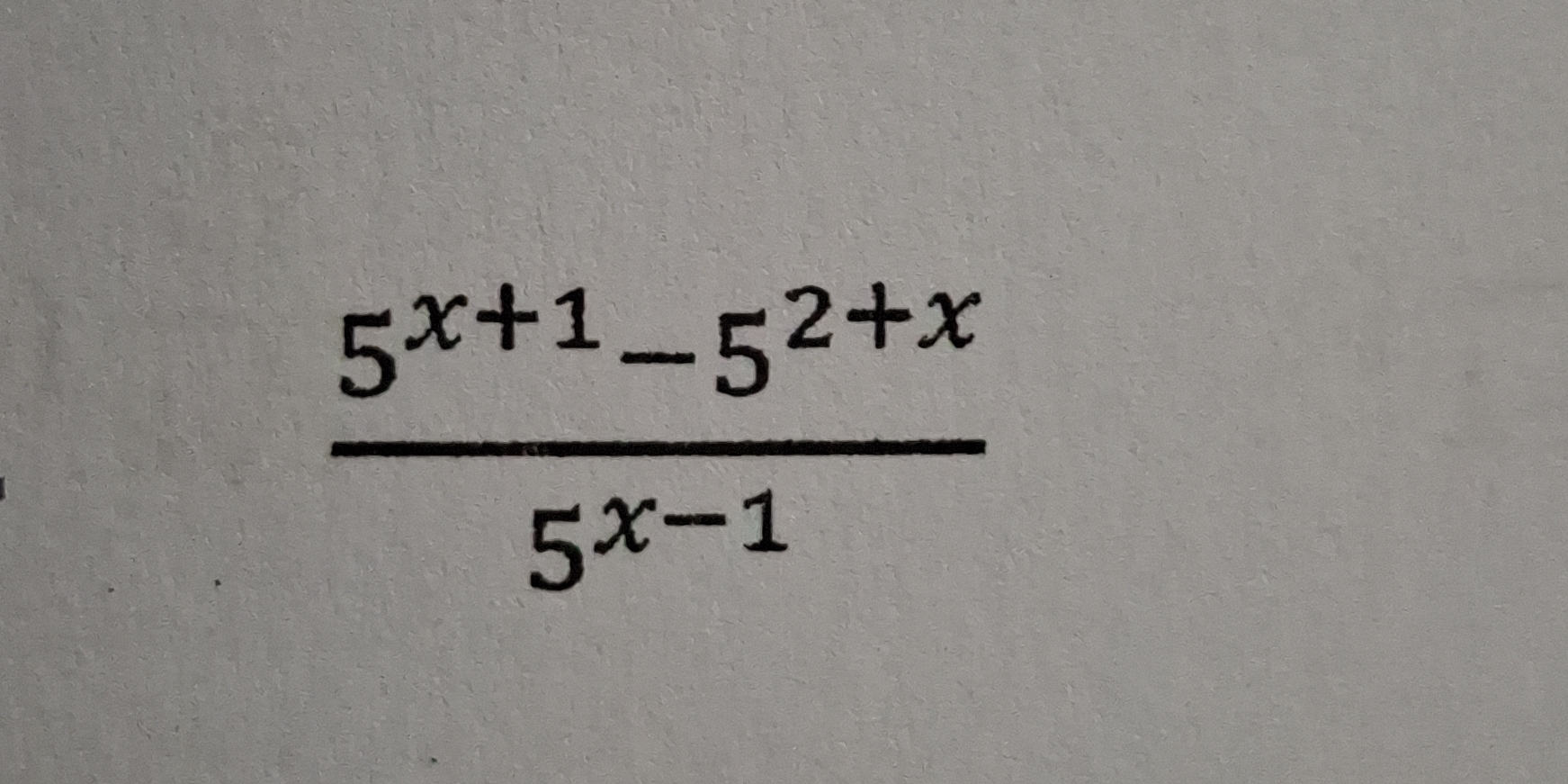
Understand the Problem
The question requires the simplification of an exponential expression. We will need to apply rules of exponents, factoring, and potentially some algebraic manipulation to reach a simplified form.
Answer
$-100$
Answer for screen readers
$-100$
Steps to Solve
- Rewrite the terms in the numerator using exponent rules
We can rewrite $5^{x+1}$ as $5^x \cdot 5^1$ and $5^{2+x}$ as $5^x \cdot 5^2$.
The expression now becomes $ \frac{5^x \cdot 5^1 - 5^x \cdot 5^2}{5^{x-1}} $
- Factor out the common term $5^x$ from the numerator
$ \frac{5^x(5^1 - 5^2)}{5^{x-1}} $
- Simplify the term inside the parenthesis
$5^1 - 5^2 = 5 - 25 = -20$
The expression is now $ \frac{5^x (-20)}{5^{x-1}} $
- Rewrite the denominator using exponent rules
$5^{x-1} = \frac{5^x}{5}$
The expression now becomes $ \frac{5^x(-20)}{\frac{5^x}{5}} $
- Simplify the fraction by dividing
Dividing by a fraction is the same as multiplying by its reciprocal.
$ \frac{5^x(-20)}{\frac{5^x}{5}} = 5^x(-20) \cdot \frac{5}{5^x} $
- Cancel out the $5^x$ terms
$ 5^x(-20) \cdot \frac{5}{5^x} = -20 \cdot 5 $
- Multiply to get the final answer
$-20 \cdot 5 = -100$
$-100$
More Information
The simplified form of the given exponential expression is $-100$. This is a constant value, meaning it does not depend on the variable $x$.
Tips
A common mistake is incorrectly applying the exponent rules, especially when factoring. Another mistake is mishandling the negative signs and not simplifying completely. Care should be taken to correctly apply the order of operations and simplify each term correctly.
AI-generated content may contain errors. Please verify critical information