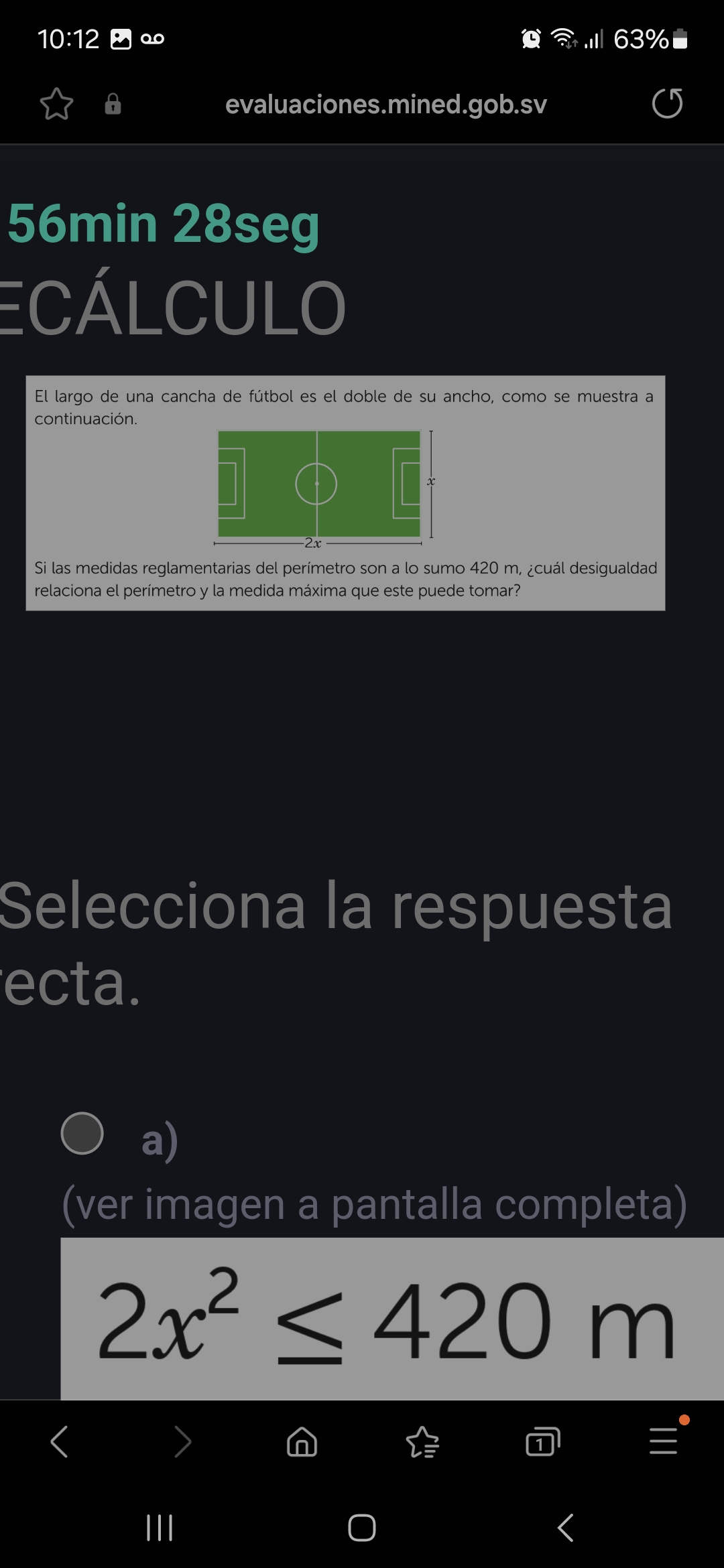
El largo de una cancha de fútbol es el doble de su ancho, como se muestra a continuación. Si las medidas reglamentarias del perímetro son a lo sumo 420 m, ¿cuál desigualdad relacio... El largo de una cancha de fútbol es el doble de su ancho, como se muestra a continuación. Si las medidas reglamentarias del perímetro son a lo sumo 420 m, ¿cuál desigualdad relaciona el perímetro y la medida máxima que este puede tomar?
Understand the Problem
La pregunta nos pide encontrar la desigualdad que relaciona el perímetro de una cancha de fútbol con su medida máxima, dado que el largo es el doble del ancho y el perímetro reglamentario es a lo sumo 420 m. Debemos establecer una ecuación para el perímetro en términos del ancho (x) y luego determinar la desigualdad correcta.
Answer
$6x \le 420$
Answer for screen readers
$6x \le 420$
Steps to Solve
- Definir las variables
Sea $x$ el ancho de la cancha. Dado que el largo es el doble del ancho, el largo es $2x$.
- Escribir la fórmula del perímetro
El perímetro $P$ de un rectángulo es la suma de todos sus lados. En este caso, $$ P = x + 2x + x + 2x $$
- Simplificar la expresión del perímetro
Simplificando la expresión anterior, obtenemos: $$ P = 6x $$
- Establecer la desigualdad
El problema dice que el perímetro es "a lo sumo" 420 m, lo que significa que el perímetro es menor o igual a 420 m. Por lo tanto, podemos escribir la desigualdad: $$ 6x \le 420 $$ Nota: La opción $2x^2 \leq 420$ es incorrecta porque representa el área de un rectángulo donde uno de sus lados es $x$ y el otro es $2x$, no el perímetro.
$6x \le 420$
More Information
La desigualdad describe la restricción sobre el perímetro de la cancha de fútbol, asegurando que no exceda el límite reglamentario de 420 metros.
Tips
Un error común es confundir el área con el perímetro, o aplicar incorrectamente la relación dada entre el largo y el ancho. En este caso, la respuesta $2x^2 \le 420$ relaciona incorrectamente el área (y no el perímetro) con la medida máxima permitida.
AI-generated content may contain errors. Please verify critical information