Si se va a colocar listón en la orilla de la falda, ¿cuántos metros de listón necesita?
Understand the Problem
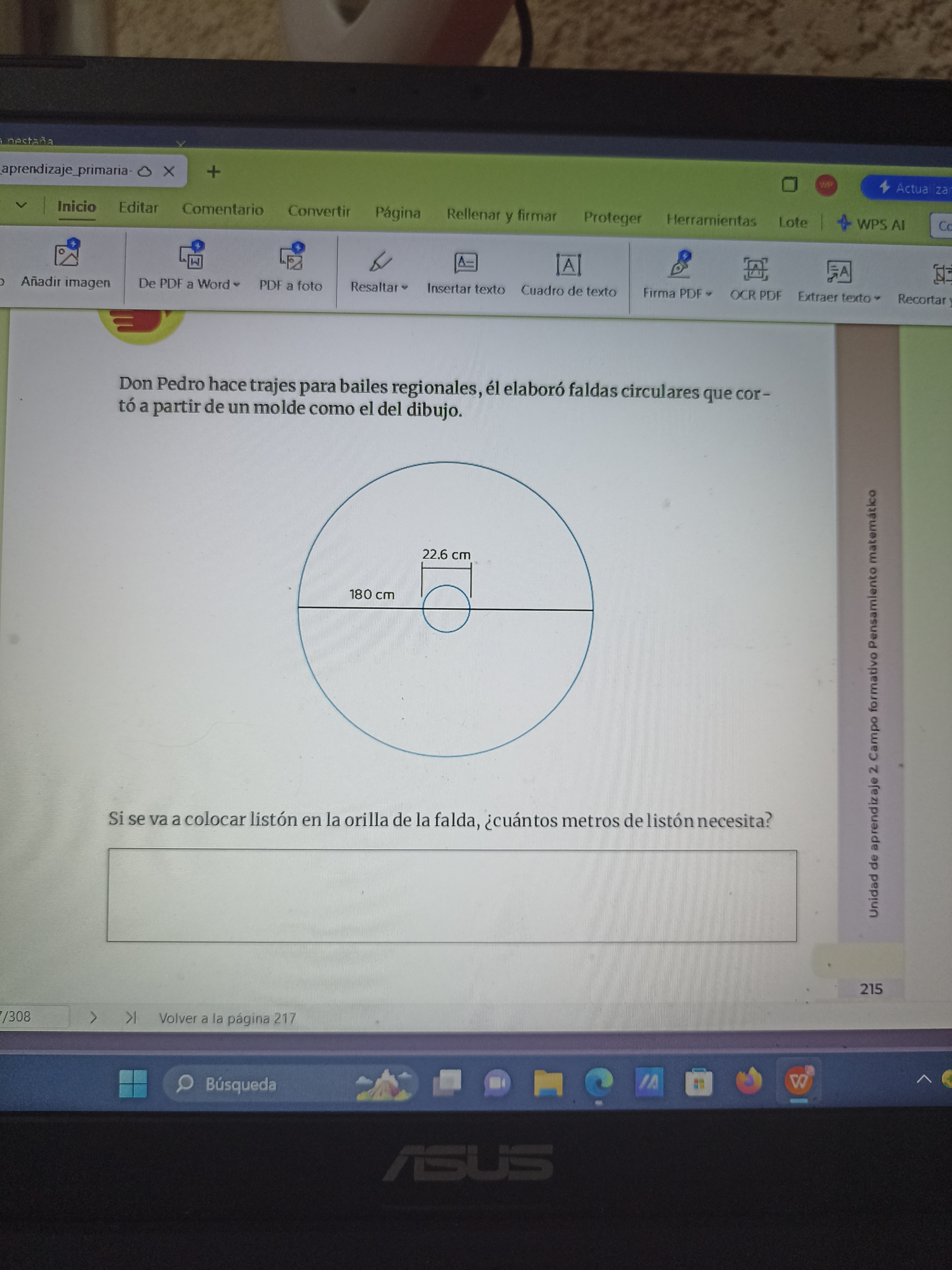
La pregunta trata sobre un problema de geometría en el que Don Pedro elaboró faldas circulares y necesitamos calcular la cantidad de listón necesaria para colocar en el borde de la falda. Para ello, debemos calcular la circunferencia del círculo exterior (falda) y restar la circunferencia del círculo interior (cintura). Luego, convertir el resultado a metros.
Answer
5. 65488
Answer for screen readers
- 65488 metros
Steps to Solve
- Calcula el radio del círculo exterior
El diámetro del círculo exterior es 180 cm, entonces el radio $r_1$ es la mitad del diámetro: $$r_1 = \frac{180}{2} = 90 \text{ cm}$$
- Calcula el radio del círculo interior
El diámetro del círculo interior es 22.6 cm, entonces el radio $r_2$ es la mitad del diámetro: $$r_2 = \frac{22.6}{2} = 11.3 \text{ cm}$$
- Calcula la circunferencia del círculo exterior
La circunferencia $C_1$ del círculo exterior se calcula con la fórmula: $$C_1 = 2 \pi r_1 = 2 \pi (90) = 180 \pi \text{ cm}$$
- Calcula la circunferencia del círculo interior
La circunferencia $C_2$ del círculo interior se calcula con la fórmula: $$C_2 = 2 \pi r_2 = 2 \pi (11.3) = 22.6 \pi \text{ cm}$$
- Calcula la cantidad de listón necesaria
La cantidad de listón necesaria es la circunferencia del círculo exterior: $$C_1 = 180 \pi \approx 180 \cdot 3.1416 \approx 565.488\text{ cm}$$
- Convierte la cantidad de listón a metros
Para convertir centímetros a metros, dividimos entre 100: $$\frac{565.488}{100} \approx 5.65488 \text{ m}$$
- 65488 metros
More Information
La cantidad total de listón que Don Pedro necesita es aproximadamente 5.65 metros.
Tips
Un error común es calcular el área en lugar de la circunferencia. Otro error es olvidar convertir de centímetros a metros.
AI-generated content may contain errors. Please verify critical information