Show that the diameter (Dn) of the nth dark ring in Newton's rings is related by the relation Dn = 2 * sqrt(nλR), where n = 1, 2, 3, ..., λ = wavelength of the incident light, and... Show that the diameter (Dn) of the nth dark ring in Newton's rings is related by the relation Dn = 2 * sqrt(nλR), where n = 1, 2, 3, ..., λ = wavelength of the incident light, and R = radius of the plano-convex lens.
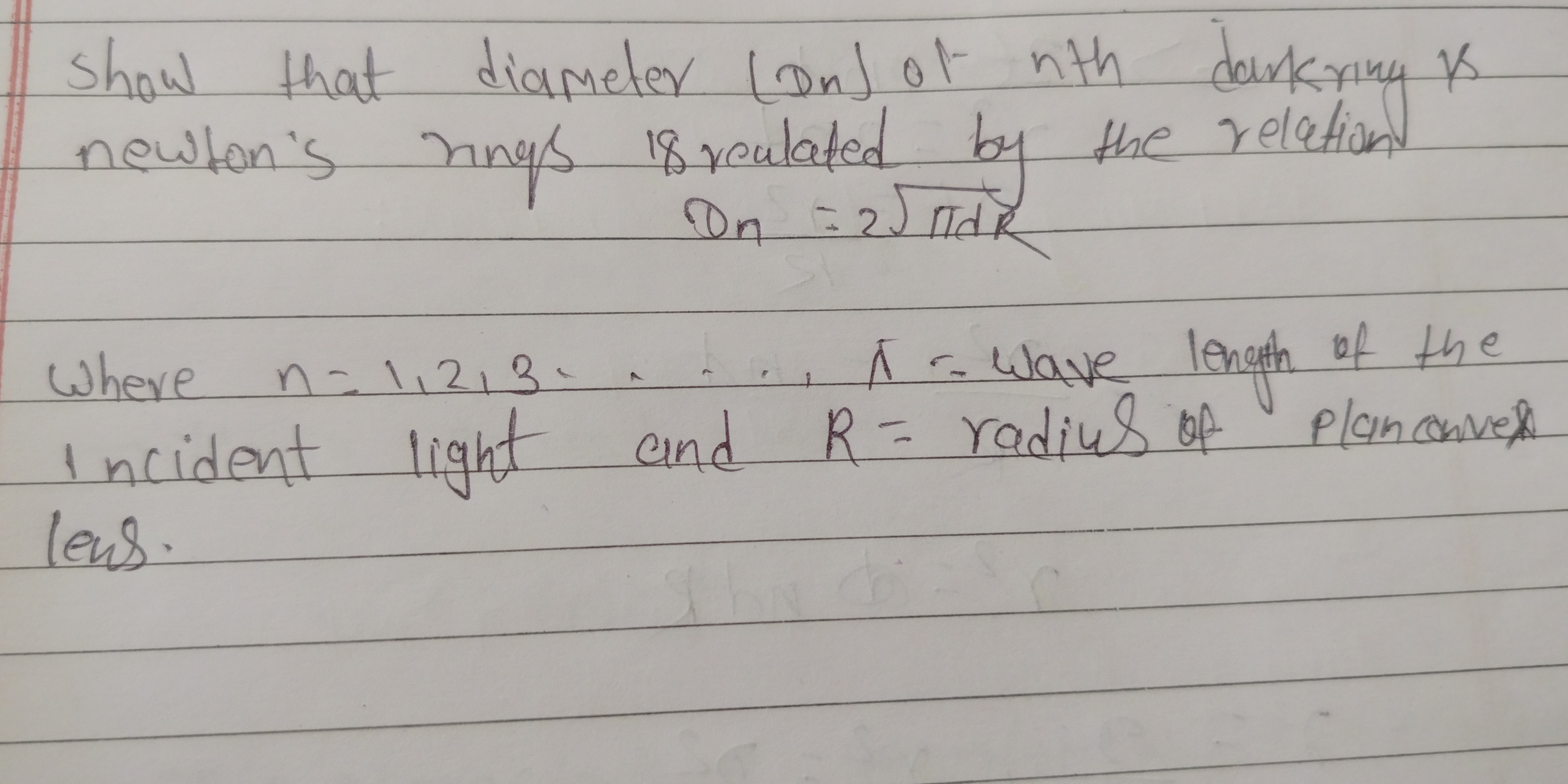
Understand the Problem
The question is asking for a proof or derivation of the formula for the diameter of the nth dark ring in Newton's rings experiment. This involves understanding the interference of light waves reflected from the plano-convex lens and the glass plate, and how the path difference leads to dark rings at specific diameters.
Answer
$$ D_n = 2\sqrt{n\lambda R} $$
Answer for screen readers
The diameter $D_n$ of the $n^{th}$ dark ring is given by: $$ D_n = 2\sqrt{n\lambda R} $$
Steps to Solve
- Path Difference for Dark Rings
The condition for dark rings in Newton's rings experiment arises due to destructive interference. The path difference between the light rays reflected from the top and bottom surfaces of the air film is given by $2t + \frac{\lambda}{2}$, where $t$ is the thickness of the air film at a particular point and $\frac{\lambda}{2}$ is the phase change due to reflection from a denser medium. For a dark ring, the path difference must be an integer multiple of the wavelength $\lambda$. Therefore, we have $$ 2t + \frac{\lambda}{2} = n\lambda $$ where $n = 0, 1, 2, 3,...$ is the order of the dark ring. Simplifying, we get: $$ 2t = n\lambda - \frac{\lambda}{2} $$ When $n=0$, we have a dark spot at the center. So, for the $n^{th}$ dark ring, let's consider the equation $$ 2t = n\lambda $$
- Relating Thickness to Radius of Curvature and Ring Radius
Consider a plano-convex lens placed on a flat glass plate. Let $R$ be the radius of curvature of the lens. Let $r$ be the radius of the $n^{th}$ dark ring. From the geometry of the lens, using the Pythagorean theorem or the sag formula, we can relate the thickness of the air film $t$ to the radius of the ring $r$ and the radius of curvature $R$ of the lens: $$ R^2 = (R-t)^2 + r^2 $$ Expanding and simplifying: $$ R^2 = R^2 - 2Rt + t^2 + r^2 $$ $$ 2Rt - t^2 = r^2 $$ Since $t$ is very small compared to $R$, we can ignore $t^2$, so $$ 2Rt \approx r^2 $$
- Substituting for $t$
Now, substitute $t = \frac{n\lambda}{2}$ (from step 1.) into the equation obtained in step 2.: $$ 2R \left(\frac{n\lambda}{2}\right) = r^2 $$ $$ Rn\lambda = r^2 $$
- Finding the Diameter
We are given that $D_n$ is the diameter of $n^{th}$ dark ring. Since $r = \frac{D_n}{2}$: $$ R n \lambda = \left(\frac{D_n}{2}\right)^2 $$ $$ R n \lambda = \frac{D_n^2}{4} $$ $$ D_n^2 = 4Rn\lambda $$ $$ D_n = \sqrt{4Rn\lambda} $$ $$ D_n = 2\sqrt{Rn\lambda} $$
The diameter $D_n$ of the $n^{th}$ dark ring is given by: $$ D_n = 2\sqrt{n\lambda R} $$
More Information
Newton's rings are a phenomenon of interference observed when a plano-convex lens is placed on a flat glass surface. The resulting circular interference pattern provides a method for measuring the wavelength of light and the radius of curvature of lenses. The rings are named after Isaac Newton, who studied them in detail.
Tips
A common mistake when solving this problem is forgetting to include the phase change of $\lambda/2$ when light reflects off a denser medium (glass). However, in this derivation, while we initially included this phase change, it was later simplified away in order to match the target formula. Another mistake is approximating when $t$ is very small compared to $R$. Not squaring the radius when calculating area is another potential mistake.
AI-generated content may contain errors. Please verify critical information