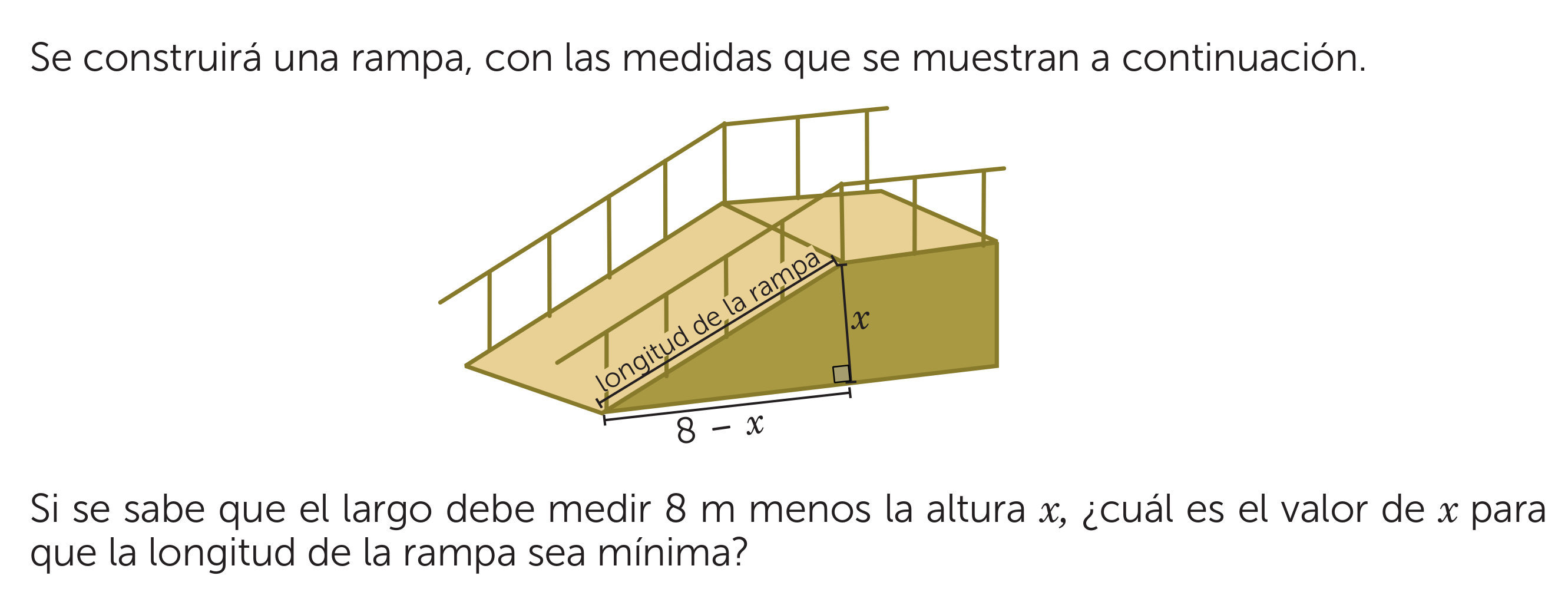
Se construirá una rampa con las medidas que se muestran a continuación. Si se sabe que el largo debe medir 8 m menos la altura x, ¿cuál es el valor de x para que la longitud de la... Se construirá una rampa con las medidas que se muestran a continuación. Si se sabe que el largo debe medir 8 m menos la altura x, ¿cuál es el valor de x para que la longitud de la rampa sea mínima?
Understand the Problem
El problema describe una rampa con una altura x y una base de 8-x. Se pide encontrar el valor de x que minimice la longitud de la rampa (la hipotenusa del triángulo rectángulo formado). Esto implica usar el teorema de Pitágoras para expresar la longitud de la rampa en función de x, y luego encontrar el mínimo de esa función, posiblemente usando cálculo diferencial.
Answer
$x=4$
Answer for screen readers
El valor de $x$ que minimiza la longitud de la rampa es $x = 4$.
Steps to Solve
- Define la longitud de la rampa usando el teorema de Pitágoras
La longitud de la rampa, $L$, es la hipotenusa del triángulo rectángulo. Usando el teorema de Pitágoras, podemos expresar $L$ en términos de $x$ como:
$$L = \sqrt{x^2 + (8-x)^2}$$
- Simplifica la expresión para la longitud
Simplificamos la expresión dentro de la raíz cuadrada:
$$L = \sqrt{x^2 + 64 - 16x + x^2} = \sqrt{2x^2 - 16x + 64}$$
- Minimiza la longitud derivando y encontrando puntos críticos
Para minimizar $L$, derivamos la función $L(x) = \sqrt{2x^2 - 16x + 64}$ con respecto a $x$ y encontramos los puntos críticos igualando la derivada a cero. Es más fácil minimizar el cuadrado de la longitud, $L^2 = 2x^2 - 16x + 64$, ya que la raíz cuadrada es una función monótona creciente. Entonces, derivamos $L^2$ respecto a $x$:
$$\frac{d(L^2)}{dx} = 4x - 16$$
Igualamos la derivada a cero para encontrar los puntos críticos:
$$4x - 16 = 0$$
$$4x = 16$$
$$x = 4$$
- Verifica que el punto crítico es un mínimo
Para verificar que $x=4$ es un mínimo, tomamos la segunda derivada de $L^2$:
$$\frac{d^2(L^2)}{dx^2} = 4$$
Ya que la segunda derivada es positiva, $x=4$ corresponde a un mínimo local.
El valor de $x$ que minimiza la longitud de la rampa es $x = 4$.
More Information
El valor de $x$ es 4 metros, lo que significa que la altura de la rampa es de 4 metros. La base de la rampa también es de 4 metros (8-4 = 4). Esto forma un triángulo rectángulo isósceles.
Tips
Un error común es olvidar simplificar la expresión antes de derivar, lo cual puede complicar el cálculo de la derivada. Otro error es no verificar que el punto crítico es un mínimo (usando la segunda derivada). También, se puede olvidar que minimizar $L^2$ es equivalente a minimizar $L$, lo cual simplifica el problema.
AI-generated content may contain errors. Please verify critical information