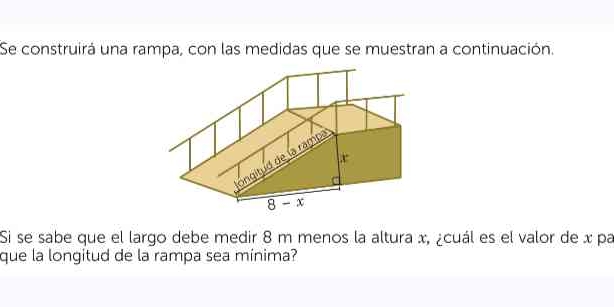
Se construirá una rampa, con las medidas que se muestran a continuación. Si se sabe que el largo (la base) debe medir 8 m menos la altura x, ¿cuál es el valor de x para que la long... Se construirá una rampa, con las medidas que se muestran a continuación. Si se sabe que el largo (la base) debe medir 8 m menos la altura x, ¿cuál es el valor de x para que la longitud de la rampa sea mínima?
Understand the Problem
El problema describe una rampa y pregunta por el valor específico de 'x' que minimiza la longitud de la rampa. Se nos da la altura de la rampa como 'x' y la base como '8-x'. Debemos usar esta información para encontrar el valor de 'x' que hace que la longitud de la rampa sea lo más pequeña posible.
Answer
$x = 4$
Answer for screen readers
El valor de $x$ para que la longitud de la rampa sea mínima es $x = 4$.
Steps to Solve
- Establecer la ecuación para la longitud de la rampa
Usando el teorema de Pitágoras, podemos expresar la longitud de la rampa $L$ en términos de $x$: $$ L(x) = \sqrt{x^2 + (8-x)^2} $$
- Minimizar la longitud al minimizar el cuadrado de la longitud
Para simplificar el cálculo, minimizaremos el cuadrado de la longitud, lo cual es equivalente a minimizar la longitud misma. Sea $f(x) = L(x)^2$: $$ f(x) = x^2 + (8-x)^2 = x^2 + 64 - 16x + x^2 = 2x^2 - 16x + 64 $$
- Encontrar el valor de $x$ donde se alcanza el mínimo
Para encontrar el mínimo, calculamos la derivada de $f(x)$ y la igualamos a cero: $$ f'(x) = 4x - 16 $$ $$ 4x - 16 = 0 $$ $$ 4x = 16 $$ $$ x = 4 $$
- Verificar que es un mínimo
Calculamos la segunda derivada de $f(x)$: $$ f''(x) = 4 $$ Dado que $f''(x) > 0$, el punto crítico $x = 4$ corresponde a un mínimo.
El valor de $x$ para que la longitud de la rampa sea mínima es $x = 4$.
More Information
El valor de $x$ que minimiza la longitud de la rampa es $4$. Esto significa que cuando la altura de la rampa es $4$ metros, y la base es también $8-4 = 4$ metros, la longitud de la rampa es la menor posible.
Tips
Un error común es complicar la función original y tratar de minimizar la raíz cuadrada directamente. Es más sencillo minimizar el cuadrado de la longitud, ya que esto evita trabajar con la raíz cuadrada y simplifica el cálculo de la derivada. También, es importante verificar que el punto crítico encontrado corresponde a un mínimo y no a un máximo, usando la segunda derivada.
AI-generated content may contain errors. Please verify critical information