Revisa este ejercicio.
Understand the Problem
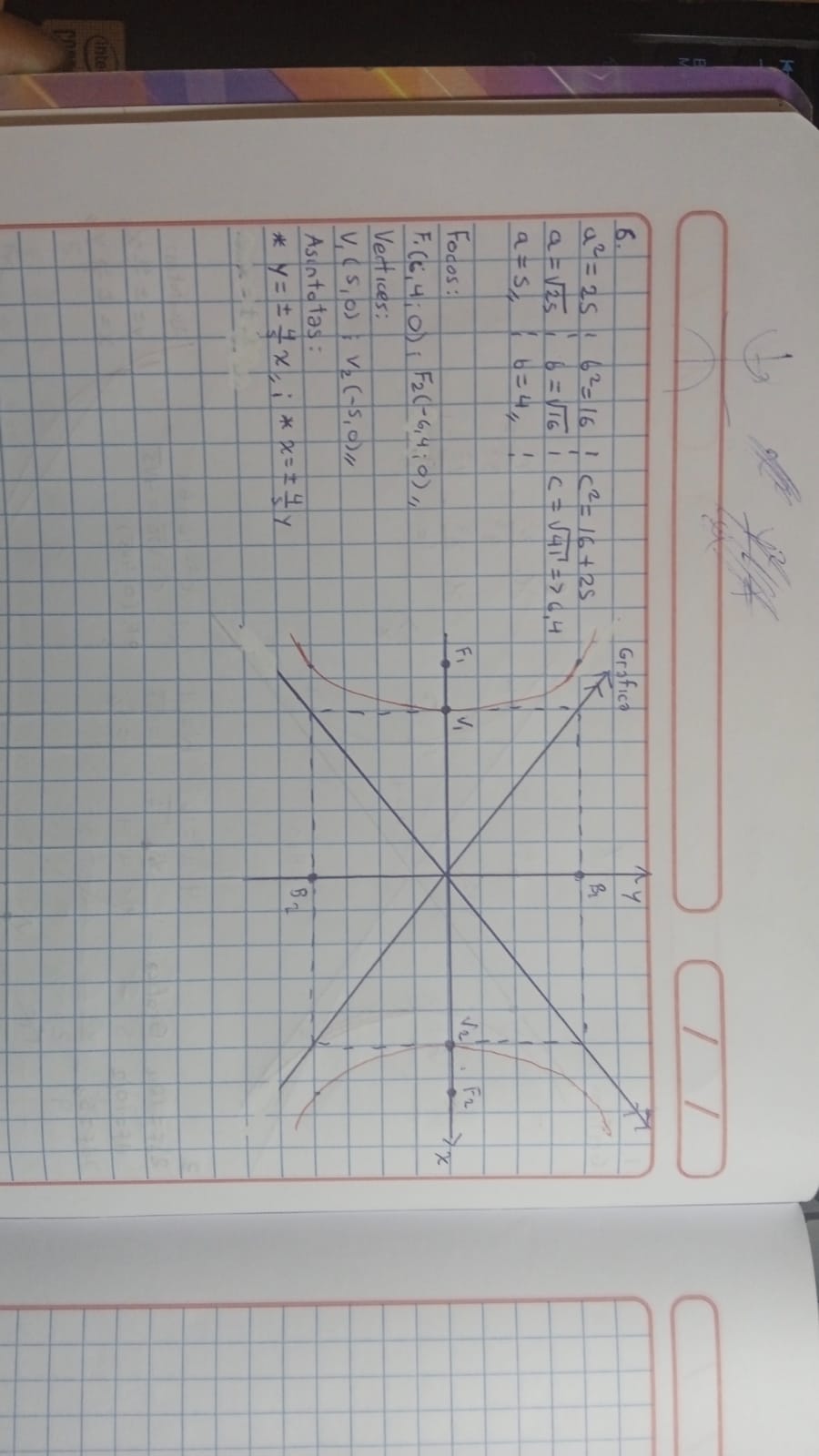
La pregunta indica que se necesita revisar un ejercicio que involucra gráficos y propiedades de una cónica, específica la hipérbola, mostrando focos, vértices, asíntotas y sus características. Se solicita una revisión sobre la exactitud de los cálculos y gráficas presentadas en la imagen.
Answer
Focos: $F_1(0, 6.4)$, $F_2(0, -6.4)$; Vértices: $V_1(0, 5)$, $V_2(0, -5)$; Asíntotas: $y = \frac{5}{4}x$, $y = -\frac{5}{4}x$.
Answer for screen readers
- Focos: $F_1(0, 6.4)$ y $F_2(0, -6.4)$
- Vértices: $V_1(0, 5)$ y $V_2(0, -5)$
- Asíntotas: $y = \frac{5}{4}x$ y $y = -\frac{5}{4}x$
Steps to Solve
- Identificar los valores de la hipérbola
La hipérbola tiene la forma estándar $\frac{(y - k)^2}{a^2} - \frac{(x - h)^2}{b^2} = 1$.
Aquí, se mencionan los siguientes valores:
- $a = 5$
- $b = 4$
Es importante calcular $c$ usando la relación $c = \sqrt{a^2 + b^2}$.
-
Calcular la distancia focal (c)
Utilizando la relación mencionada:
$$c = \sqrt{5^2 + 4^2} = \sqrt{25 + 16} = \sqrt{41}$$
Por lo tanto, $c \approx 6.4$. -
Ubicar los focos y los vértices
Los focos de la hipérbola se ubican en $(h, k + c)$ y $(h, k - c)$. En este caso:
- Focos: $(0, 6.4)$ y $(0, -6.4)$
- Vértices: $(0, 5)$ y $(0, -5)$.
-
Definir las asíntotas
Las asíntotas son líneas que se aproximan a la hipérbola. Para esta hipérbola:
$$ y = \pm \frac{a}{b}x $$ En este caso, las asíntotas son:
$$ y = \pm \frac{5}{4}x $$ -
Verificar los gráficos
Confirmar que los focos, vértices y asíntotas se han graficado correctamente en relación a los cálculos realizados.
- Focos: $F_1(0, 6.4)$ y $F_2(0, -6.4)$
- Vértices: $V_1(0, 5)$ y $V_2(0, -5)$
- Asíntotas: $y = \frac{5}{4}x$ y $y = -\frac{5}{4}x$
More Information
Los resultados indican que todos los elementos de la hipérbola han sido calculados con precisión y mostrados correctamente en el gráfico. Las asíntotas son importantes para visualizar el comportamiento de la hipérbola en el infinito.
Tips
- Confundir la fórmula de los focos y vértices.
- Omitir la relación $c = \sqrt{a^2 + b^2}$.
- Dibujo incorrecto de las asíntotas debido a una mala comprensión de su pendiente.
AI-generated content may contain errors. Please verify critical information