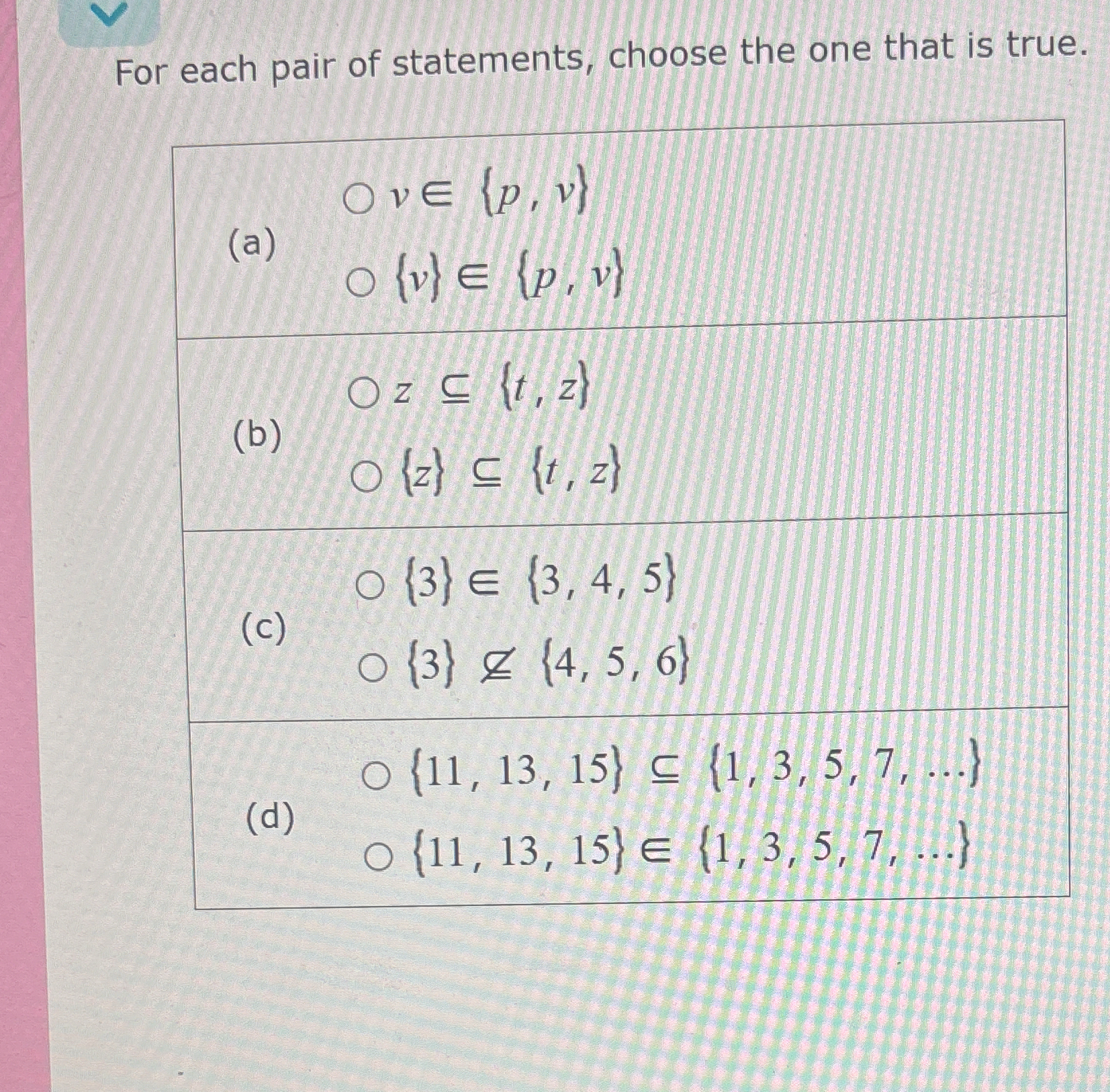
For each pair of statements, choose the one that is true: (a) v ∈ {p, v} or {v} ∈ {p, v} (b) z ⊆ {t, z} or {z} ⊆ {t, z} (c) {3} ∈ {3, 4, 5} or {3} ∉ {4, 5, 6} (d) {11, 13, 15} ⊆ {1... For each pair of statements, choose the one that is true: (a) v ∈ {p, v} or {v} ∈ {p, v} (b) z ⊆ {t, z} or {z} ⊆ {t, z} (c) {3} ∈ {3, 4, 5} or {3} ∉ {4, 5, 6} (d) {11, 13, 15} ⊆ {1, 3, 5, 7, ...} or {11, 13, 15} ∈ {1, 3, 5, 7, ...} Read more

Steps to Solve

1. Evaluating statement (a)

• $v \in {p, v}$: This statement means "v is an element of the set containing p and v." This is true because $v$ is indeed listed as one of the elements in the set ${p, v}$.
• ${v} \in {p, v}$: This statement means "the set containing only v is an element of the set containing p and v." This is false because the elements of the set ${p, v}$ are $p$ and $v$, not the set ${v}$.

2. Evaluating statement (b)

• $z \subseteq {t, z}$: This statement means "the set containing z is a subset of the set containing t and z". The set containing z is ${z}$. For ${z}$ to be a subset of ${t, z}$, every element in ${z}$ must also be in ${t, z}$. Since $z$ is in ${t, z}$, the statement ${z} \subseteq {t, z}$ is true. Note that the problem wrote $z \subseteq {t, z}$ which treats $z$ as if it were a set already, which is incorrect.
• ${z} \subseteq {t, z}$: This statement means "the set containing $z$ is a subset of the set containing $t$ and $z$". This is true, as discussed above.

3. Evaluating statement (c)

• ${3} \in {3, 4, 5}$: This statement means "the set containing 3 is an element of the set containing 3, 4, and 5." This is false. The elements of the set ${3, 4, 5}$ are $3$, $4$, and $5$, not the set ${3}$.
• ${3} \notin {4, 5, 6}$: This statement means "the set containing 3 is not an element of the set containing 4, 5, and 6." This is true because the elements of ${4, 5, 6}$ are $4$, $5$, and $6$, and ${3}$ is not among them. Also, $3 \notin {4, 5, 6}$ is true as well.

4. Evaluating statement (d)

• ${11, 13, 15} \subseteq {1, 3, 5, 7, ...}$: This statement means "the set containing 11, 13, and 15 is a subset of the set of all positive odd integers." This is true because 11, 13, and 15 are all positive odd integers.
• ${11, 13, 15} \in {1, 3, 5, 7, ...}$: This statement means "the set containing 11, 13, and 15 is an element of the set of all positive odd integers." This is false because the elements of the set ${1, 3, 5, 7, ...}$ are individual odd numbers, not sets of odd numbers.