Prove the identity: \frac{\sin \theta \csc \theta}{\cot \theta} = \tan \theta
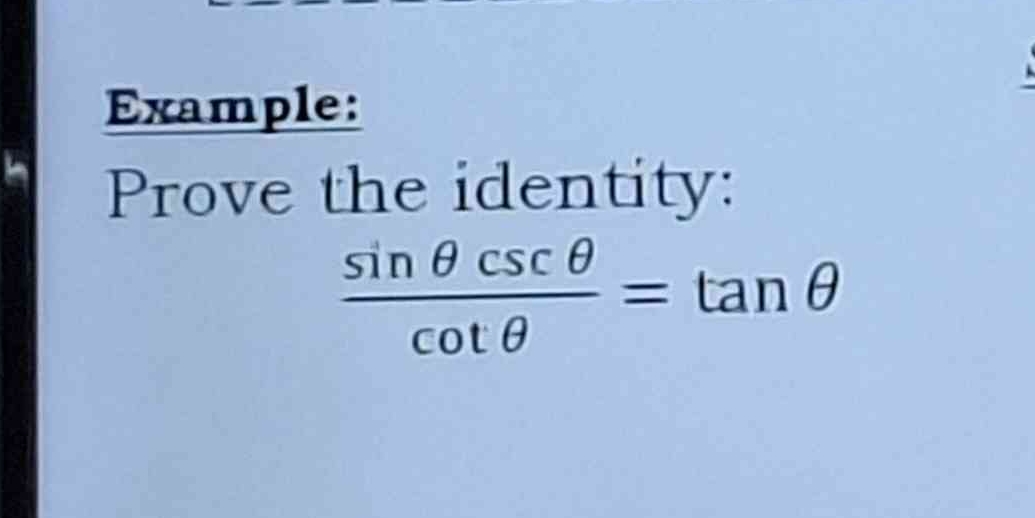
Understand the Problem
The question is asking to prove the given trigonometric identity involving sine, cosecant, and cotangent functions, showing that the left-hand side simplifies to the right-hand side.
Answer
$$ \frac{\sin \theta \csc \theta}{\cot \theta} = \tan \theta $$
Answer for screen readers
The identity is proven as: $$ \frac{\sin \theta \csc \theta}{\cot \theta} = \tan \theta $$
Steps to Solve
- Rewrite the functions in basic terms
Start with the left-hand side of the identity: $$ \frac{\sin \theta \csc \theta}{\cot \theta} $$
Recall that:
- The cosecant function is defined as $ \csc \theta = \frac{1}{\sin \theta} $.
- The cotangent function is defined as $ \cot \theta = \frac{\cos \theta}{\sin \theta} $.
- Substitute the definitions
Substituting the definitions into the expression: $$ \frac{\sin \theta \cdot \frac{1}{\sin \theta}}{\frac{\cos \theta}{\sin \theta}} $$
- Simplify the expression
This simplifies to: $$ \frac{1}{\frac{\cos \theta}{\sin \theta}} = \frac{1 \cdot \sin \theta}{\cos \theta} $$
- Use basic trigonometric identities
This expression can be rewritten as: $$ \frac{\sin \theta}{\cos \theta} = \tan \theta $$
- Conclude the proof
Thus, we have shown that: $$ \frac{\sin \theta \csc \theta}{\cot \theta} = \tan \theta $$
The identity is proven as: $$ \frac{\sin \theta \csc \theta}{\cot \theta} = \tan \theta $$
More Information
This identity is useful in various trigonometry problems and establishing relationships between different trigonometric functions. Understanding these identities helps simplify complex trigonometric expressions in mathematics.
Tips
- Forgetting to use the definitions of trigonometric functions correctly.
- Failing to simplify the expression fully, leaving it in a fraction form without recognizing it can reduce further.
AI-generated content may contain errors. Please verify critical information