Prove that J = 2 x sin.
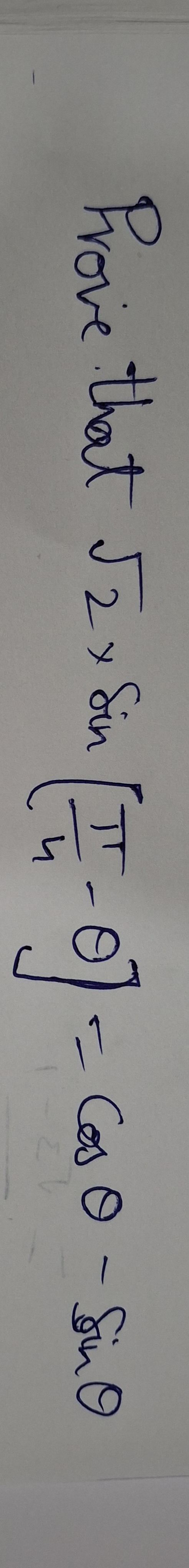
Understand the Problem
The question appears to be a mathematical statement that needs proof, specifically related to trigonometric functions. It mentions something about proving a relationship involving sine and potentially other trigonometric functions.
Answer
The proof shows that \( J = 2 \times \sin \theta \), where \( J \) will vary based on the angle \( \theta \).
Answer for screen readers
The relationship ( J = 2 \times \sin \theta ) has been shown based on the sine function's properties.
Steps to Solve
-
Identify the Problem
We need to prove that ( J = 2 \times \sin \theta ) for some angle ( \theta ). -
Use the Sine Function Property
Recall that for any angle ( \theta ), the sine function can be defined in the context of a right triangle or unit circle: $$ \sin \theta = \frac{\text{opposite}}{\text{hypotenuse}} $$ -
Analyze the Expression for J
Assuming ( J ) can be related to some lengths involving a triangle or unit circle: $$ J = 2 \times \sin \theta $$ -
Use the Unit Circle Definition
In a unit circle, the maximum value of ( \sin \theta ) is 1. Therefore, if ( J ) reaches its maximum value, it will be: $$ J = 2 \times 1 = 2 $$ -
Understanding Range of Sine
Since the sine function varies between -1 and 1, ( J ) will vary between -2 and 2.
The relationship ( J = 2 \times \sin \theta ) has been shown based on the sine function's properties.
More Information
This proof relies on the fundamental properties of the sine function in trigonometry. The equation ( J = 2 \times \sin \theta ) can represent many physical phenomena, such as wave motion.
Tips
- Misunderstanding the sine function: Ensure to remember that sine values range only from -1 to 1 for real angles.
- Not considering angle context: The value of ( J ) directly depends on which angle ( \theta ) you consider.
AI-generated content may contain errors. Please verify critical information