Evaluate the expression: 1 / (2^-4)
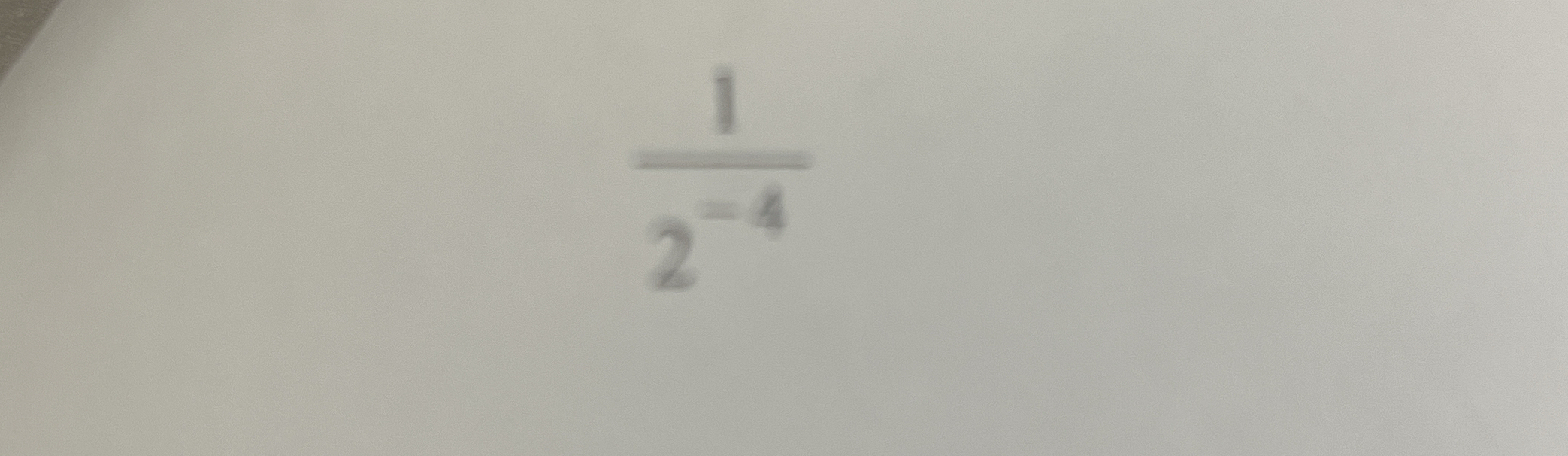
Understand the Problem
The question asks us to evaluate the expression 1 / (2 to the power of -4). This involves understanding negative exponents and how to simplify them.
Answer
16
Answer for screen readers
16
Steps to Solve
- Rewrite the expression
The original expression is $\frac{1}{2^{-4}}$.
- Apply the negative exponent rule
A negative exponent means taking the reciprocal of the base raised to the positive exponent. Specifically, $a^{-n} = \frac{1}{a^n}$. Therefore, $2^{-4} = \frac{1}{2^4}$.
- Substitute back into the original expression
The expression becomes $\frac{1}{\frac{1}{2^4}}$.
- Simplify the complex fraction
Dividing by a fraction is the same as multiplying by its reciprocal. So, $\frac{1}{\frac{1}{2^4}} = 1 \cdot \frac{2^4}{1} = 2^4$.
- Calculate $2^4$
$2^4 = 2 \cdot 2 \cdot 2 \cdot 2 = 16$.
16
More Information
The expression $\frac{1}{2^{-4}}$ simplifies to 16.
Tips
A common mistake is misinterpreting the negative exponent and incorrectly calculating $2^{-4}$. Another mistake is not understanding how to simplify a complex fraction.
AI-generated content may contain errors. Please verify critical information