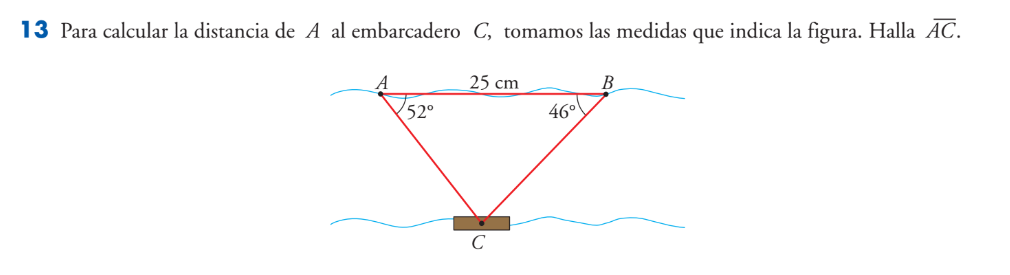
Para calcular la distancia de A al embarcadero C, tomamos las medidas que indica la figura. Halla AC.

Steps to Solve

1. Find the angle at C

Since the sum of the angles in a triangle is $180^\circ$, we can find the angle at $C$ by subtracting the angles at $A$ ($52^\circ$) and $B$ ($46^\circ$) from $180^\circ$: $$ \angle C = 180^\circ - 52^\circ - 46^\circ = 82^\circ $$

2. Apply the Law of Sines

We can use the Law of Sines to find the length of $AC$. The Law of Sines states that for any triangle, the ratio of the length of a side to the sine of its opposite angle is constant. In this case, we have: $$ \frac{AC}{\sin(\angle B)} = \frac{AB}{\sin(\angle C)} $$ We are given $AB = 25$ cm, $\angle B = 46^\circ$, and we calculated $\angle C = 82^\circ$. Plugging these values into the equation, we get: $$ \frac{AC}{\sin(46^\circ)} = \frac{25}{\sin(82^\circ)} $$

3. Solve for $AC$

To find $AC$, we multiply both sides of the equation by $\sin(46^\circ)$: $$ AC = \frac{25 \cdot \sin(46^\circ)}{\sin(82^\circ)} $$ Now, we can use a calculator to find the values of the sines and compute $AC$: $$ AC \approx \frac{25 \cdot 0.7193}{0.9903} \approx \frac{17.9825}{0.9903} \approx 18.158 $$ Therefore, the length of $AC$ is approximately 18.16 cm.