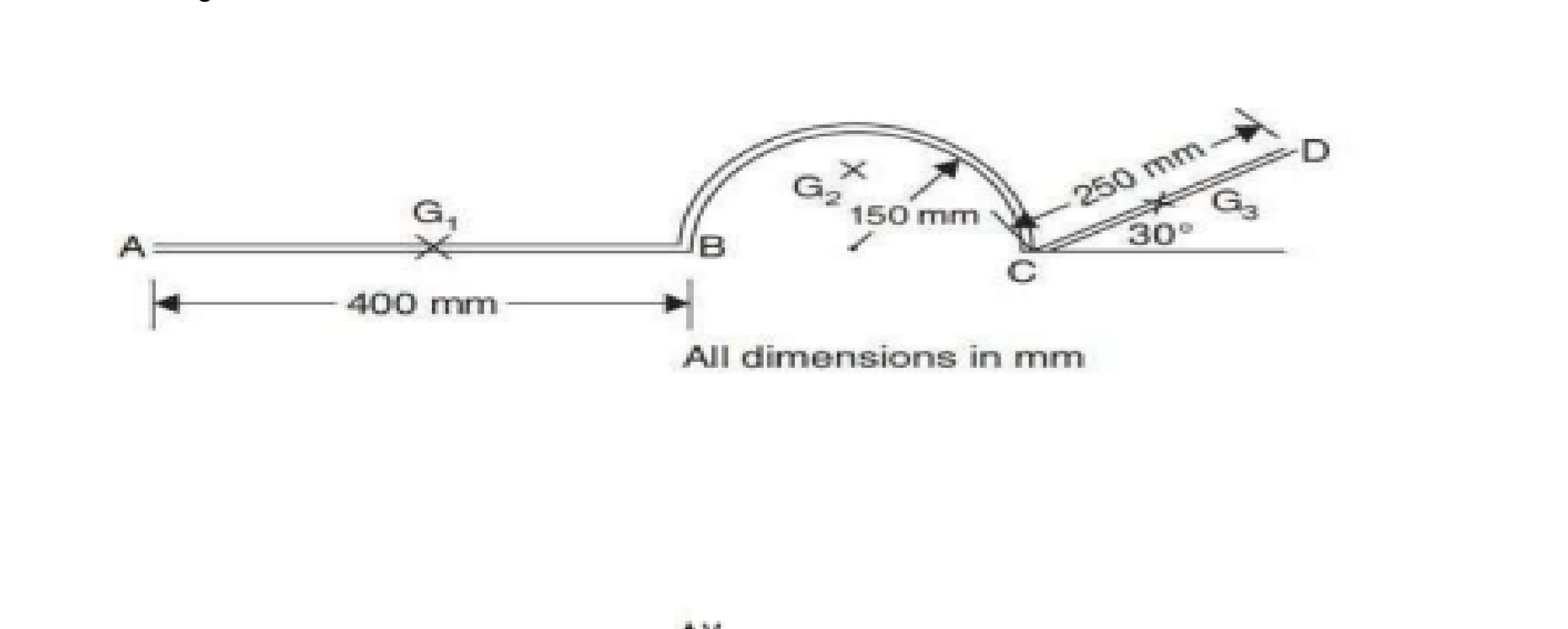
Obtain CG for the following laminas shown in the figure.

Steps to Solve

1. Identify Dimensions and Areas

   Identify the geometric shapes and their corresponding dimensions from the diagram. The structure can be divided into three parts:

   • Rectangle (from A to B): Height = $G_1$
   • Circular arc (from B to C): Radius = $150 , mm$
   • Triangle (from C to D): Base = $250 , mm$, Height derived from angle $30^\circ$.

2. Calculate Areas of Each Section

   For the rectangle: $$ A_1 = \text{Height} \times \text{Width} = G_1 \times 400 $$

   For the circular arc: $$ A_2 = \pi r^2 $$ where $r = 150 , mm$.

   For the triangle, use the formula for the area of a triangle: $$ A_3 = \frac{1}{2} \times \text{Base} \times \text{Height} $$ Here, the height can be calculated from the triangle's angle as: $$ \text{Height} = 250 \times \sin(30^\circ) $$

3. Determine the Centroid of Each Section

   For the rectangle: $$ x_{G1} = \frac{400}{2} = 200 , mm $$

   For the circular arc: The centroid is at a distance from B equal to the radius: $$ x_{G2} = 400 + 150 = 550 , mm $$

   For the triangle: The centroid is located at one-third of the base from the larger side: $$ x_{G3} = 400 + \frac{250}{3} , mm $$

4. Calculate the Overall Center of Gravity

   Use the formula for the centroid of combined areas: $$ x_{CG} = \frac{(A_1 \cdot x_{G1}) + (A_2 \cdot x_{G2}) + (A_3 \cdot x_{G3})}{A_1 + A_2 + A_3} $$

5. Substitute Values and Solve

   Substitute the calculated areas and centroids into the equation for $x_{CG}$, and simplify to find the desired center of gravity for the structure.