Note that f is continuous on [0,3]. f(0) = 1 - 0 + sin(0) = 1. f(3) = 2 - 3 + sin(3 \pi) = -1. So by IVT, there exists c in (0,3) such that f(c) = 0.

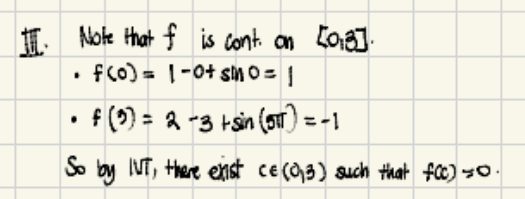
Understand the Problem

The image shows an application of the Intermediate Value Theorem (IVT). It begins by noting that a function 'f' is continuous on the closed interval [0, 3]. Then, it calculates the value of 'f' at 0 and 3. Finally, it concludes that there exists a 'c' in the open interval (0, 3) such that f(c) = 0, based on the IVT.

Answer

By the Intermediate Value Theorem, there exists a $c \in (0, 3)$ such that $f(c) = 0$ because $f(0) = 1$ and $f(3) = -2$.

Steps to Solve

Identify the function and interval

The function $f$ is continuous on the closed interval $[0, 3]$. We need to consider the function $f(x) = 1 - x + \sin(\pi x)$.

Evaluate $f(0)$

$f(0) = 1 - 0 + \sin(\pi \cdot 0) = 1 - 0 + \sin(0) = 1 - 0 + 0 = 1$

Evaluate $f(3)$

$f(3) = 1 - 3 + \sin(\pi \cdot 3) = 1 - 3 + \sin(3\pi) = -2 + 0 = -2$

Apply the Intermediate Value Theorem (IVT)

Since $f(0) = 1$ and $f(3) = -2$, and since $f$ is continuous on $[0, 3]$, by the IVT, there exists a $c$ in the open interval $(0, 3)$ such that $f(c) = 0$ because $0$ is between $f(0)$ and $f(3)$.

By the Intermediate Value Theorem, there exists a $c \in (0, 3)$ such that $f(c) = 0$ because $f(0) = 1$ and $f(3) = -2$.

More Information

The Intermediate Value Theorem states that if a continuous function $f$ achieves two values $f(a)$ and $f(b)$ on an interval $[a, b]$, then it also takes on every value between $f(a)$ and $f(b)$ at some point within that interval. In this case, since $f(0) = 1$ and $f(3) = -2$, the function must take on the value $0$ at some point $c$ in the interval $(0, 3)$.

Tips

A common mistake is to miscalculate $f(3)$. Remember that $f(3) = 1 - 3 + \sin(3\pi)$, and $\sin(3\pi) = 0$, so $f(3) = -2$, not $-1$.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!