Multiply the following complex numbers: (-3 + 0.6j)(0.4j - 7)
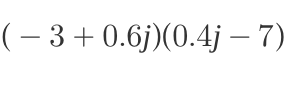
Understand the Problem
The question asks to multiply two complex numbers expressed in rectangular form. We will use the distributive property (FOIL method) and simplify, remembering that j^2 = -1.
Answer
$20.76 - 5.4j$
Answer for screen readers
$20.76 - 5.4j$
Steps to Solve
-
Apply the distributive property (FOIL method) Expand the expression by multiplying each term in the first complex number by each term in the second complex number: $(-3 + 0.6j)(0.4j - 7) = (-3)(0.4j) + (-3)(-7) + (0.6j)(0.4j) + (0.6j)(-7)$
-
Perform the multiplications Multiply the terms: $-1.2j + 21 + 0.24j^2 - 4.2j$
-
Substitute $j^2 = -1$ Replace $j^2$ with $-1$: $-1.2j + 21 + 0.24(-1) - 4.2j$
-
Simplify the expression Combine the real and imaginary parts: $-1.2j + 21 - 0.24 - 4.2j = (21 - 0.24) + (-1.2j - 4.2j)$
-
Combine like terms Combine real and imaginary numbers: $20.76 - 5.4j$
$20.76 - 5.4j$
More Information
The result is a complex number in rectangular form, where 20.76 is the real part and -5.4 is the imaginary part.
Tips
A common mistake is forgetting that $j^2 = -1$. Another common mistake is incorrectly applying the distributive property or making arithmetic errors when multiplying the terms. Additionally, mistakes can occur when combining like terms (real and imaginary parts).
AI-generated content may contain errors. Please verify critical information