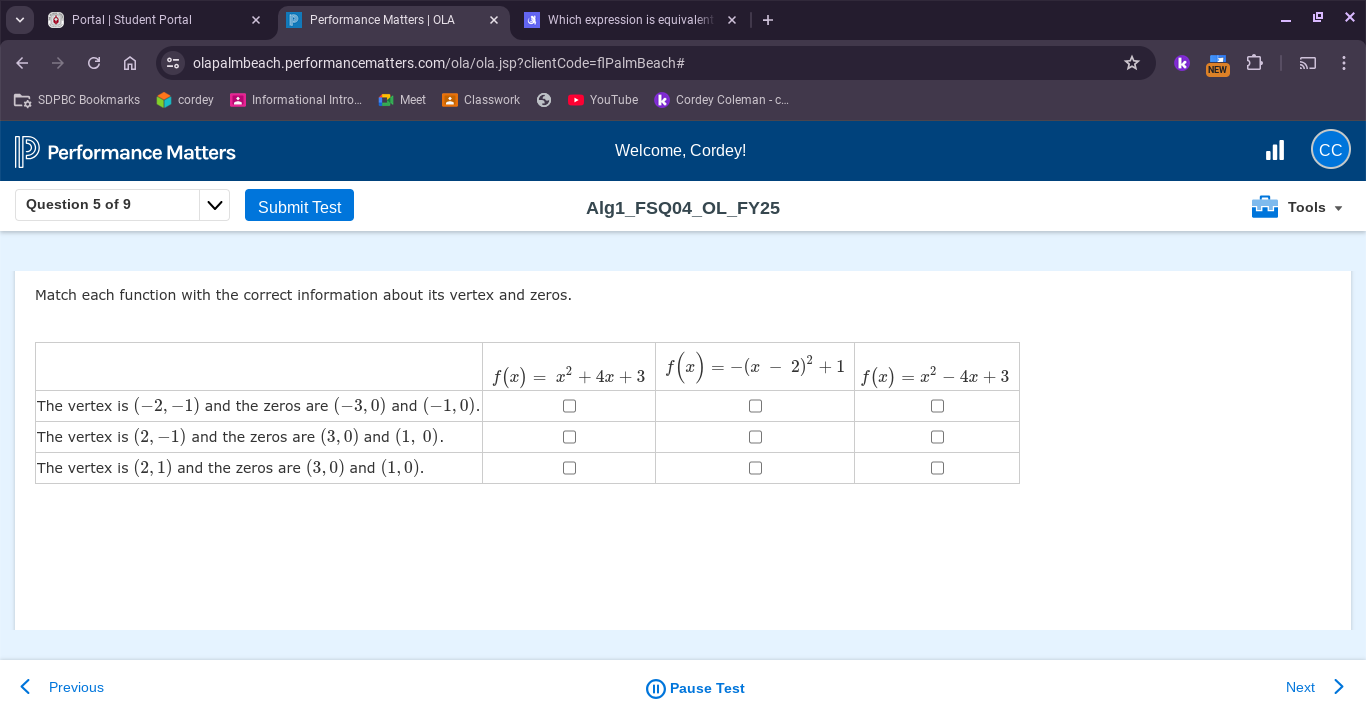
Match each function with the correct information about its vertex and zeros: Functions: f(x) = x^2 + 4x + 3 f(x) = -(x - 2)^2 + 1 f(x) = x^2 - 4x + 3 Vertex and Zeros: The vertex... Match each function with the correct information about its vertex and zeros: Functions: f(x) = x^2 + 4x + 3 f(x) = -(x - 2)^2 + 1 f(x) = x^2 - 4x + 3 Vertex and Zeros: The vertex is (-2, -1) and the zeros are (-3, 0) and (-1, 0). The vertex is (2, -1) and the zeros are (3, 0) and (1, 0). The vertex is (2, 1) and the zeros are (3, 0) and (1, 0).
Understand the Problem
The question asks to match each quadratic function with the correct information about its vertex and zeros. This involves finding the vertex and zeros (roots) for each given function and then matching them with the corresponding description.
Answer
$f(x) = x^2 + 4x + 3$ matches "The vertex is (-2,-1) and the zeros are (-3, 0) and (-1,0)". $f(x) = -(x - 2)^2 + 1$ matches "The vertex is (2, 1) and the zeros are (3,0) and (1,0)". $f(x) = x^2 - 4x + 3$ matches "The vertex is (2,-1) and the zeros are (3,0) and (1, 0)".
Answer for screen readers
$f(x) = x^2 + 4x + 3$ matches "The vertex is (-2,-1) and the zeros are (-3, 0) and (-1,0)". $f(x) = -(x - 2)^2 + 1$ matches "The vertex is (2, 1) and the zeros are (3,0) and (1,0)". $f(x) = x^2 - 4x + 3$ matches "The vertex is (2,-1) and the zeros are (3,0) and (1, 0)".
Steps to Solve
- Analyze the first quadratic function: $f(x) = x^2 + 4x + 3$
To find the vertex, we complete the square. $f(x) = x^2 + 4x + 3 = (x^2 + 4x + 4) - 4 + 3 = (x + 2)^2 - 1$ So the vertex is $(-2, -1)$. To find the zeros, we solve $f(x) = 0$: $x^2 + 4x + 3 = 0$ $(x + 3)(x + 1) = 0$ $x = -3$ or $x = -1$ So the zeros are $(-3, 0)$ and $(-1, 0)$. Therefore, this function matches with "The vertex is (-2,-1) and the zeros are (-3, 0) and (-1,0)".
- Analyze the second quadratic function: $f(x) = -(x - 2)^2 + 1$
This function is already in vertex form, $f(x) = a(x - h)^2 + k$, where $(h, k)$ is the vertex. So the vertex is $(2, 1)$. To find the zeros, we solve $f(x) = 0$: $-(x - 2)^2 + 1 = 0$ $(x - 2)^2 = 1$ $x - 2 = \pm 1$ $x = 2 + 1 = 3$ or $x = 2 - 1 = 1$ So the zeros are $(3, 0)$ and $(1, 0)$. Therefore, this function matches with "The vertex is (2, 1) and the zeros are (3,0) and (1,0)".
- Analyze the third quadratic function: $f(x) = x^2 - 4x + 3$
To find the vertex, we complete the square. $f(x) = x^2 - 4x + 3 = (x^2 - 4x + 4) - 4 + 3 = (x - 2)^2 - 1$ So the vertex is $(2, -1)$. To find the zeros, we solve $f(x) = 0$: $x^2 - 4x + 3 = 0$ $(x - 3)(x - 1) = 0$ $x = 3$ or $x = 1$ So the zeros are $(3, 0)$ and $(1, 0)$. Therefore, this function matches with "The vertex is (2,-1) and the zeros are (3,0) and (1, 0)".
$f(x) = x^2 + 4x + 3$ matches "The vertex is (-2,-1) and the zeros are (-3, 0) and (-1,0)". $f(x) = -(x - 2)^2 + 1$ matches "The vertex is (2, 1) and the zeros are (3,0) and (1,0)". $f(x) = x^2 - 4x + 3$ matches "The vertex is (2,-1) and the zeros are (3,0) and (1, 0)".
More Information
Matching each quadratic to the correct information about its vertex and zeros gives a full picture of the quadratic's characteristics.
Tips
A common mistake is incorrectly identifying the vertex when the equation is in vertex form or when completing the square. Also, errors can occur during the factoring process to find the zeros. Paying close attention to the signs is crucial.
AI-generated content may contain errors. Please verify critical information