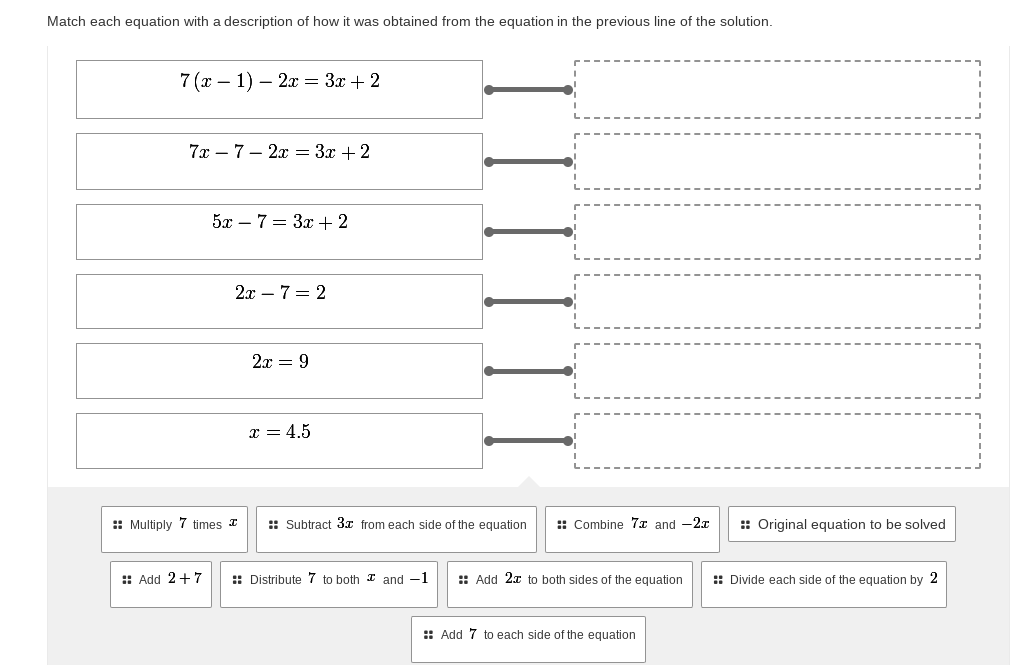
Match each equation with a description of how it was obtained from the equation in the previous line of the solution.

Understand the Problem

The question is asking to match each given equation with a description of how it was modified or derived from the previous equation in the solution process. This involves understanding algebraic manipulations and transformations.

Answer

1. Original equation to be solved 2. Distribute $ 7 $ to both $ x $ and $ -1 $ 3. Combine $ 7x $ and $-2x$ 4. Add $ 7 $ to both sides of the equation 5. Subtract $ 3x $ from each side of the equation 6. Divide each side of the equation by $ 2 $

Steps to Solve

Start with the Original Equation

The original equation is

$$ 7(x - 1) - 2x = 3x + 2 $$

Distribute the 7

To simplify, distribute the 7:

$$ 7x - 7 - 2x = 3x + 2 $$

This corresponds to "Distribute ( 7 ) to both ( x ) and ( -1 )."

Combine like terms on the left side

Combine ( 7x ) and ( -2x ):

$$ 5x - 7 = 3x + 2 $$

This step relates to "Combine ( 7x ) and (-2x)."

Add 7 to both sides of the equation

To isolate terms involving ( x ):

$$ 5x = 3x + 9 $$

This corresponds to "Add ( 7 ) to each side of the equation."

Subtract ( 3x ) from each side of the equation

Next, isolate ( x ):

$$ 2x = 9 $$

This corresponds to "Subtract ( 3x ) from each side of the equation."

Divide each side of the equation by 2

To solve for ( x ):

$$ x = 4.5 $$

This relates to "Divide each side of the equation by ( 2 )."

The matched pairs are as follows:

( 7(x - 1) - 2x = 3x + 2 ) - Original equation to be solved
( 7x - 7 - 2x = 3x + 2 ) - Distribute ( 7 ) to both ( x ) and ( -1 )
( 5x - 7 = 3x + 2 ) - Combine ( 7x ) and (-2x)
( 2x - 7 = 2 ) - Add ( 7 ) to both sides of the equation
( 2x = 9 ) - Subtract ( 3x ) from each side of the equation
( x = 4.5 ) - Divide each side of the equation by ( 2 )

More Information

This problem illustrates the process of manipulating equations step-by-step, showcasing how each algebraic operation can be linked to its respective transformation of the equation. Understanding these transformations is essential for solving linear equations.

Tips

Mixing up the order of operations: Ensure the correct sequence of operations is followed.
Forgetting to perform the same operation on both sides of the equation: This can lead to incorrect solutions.
Misapplying distribution: Always double-check that distribution is applied correctly to all terms.

Thank you for voting!