Solve the system of equations: x - 2y = 3 x^2 - xy - y^2 = 1
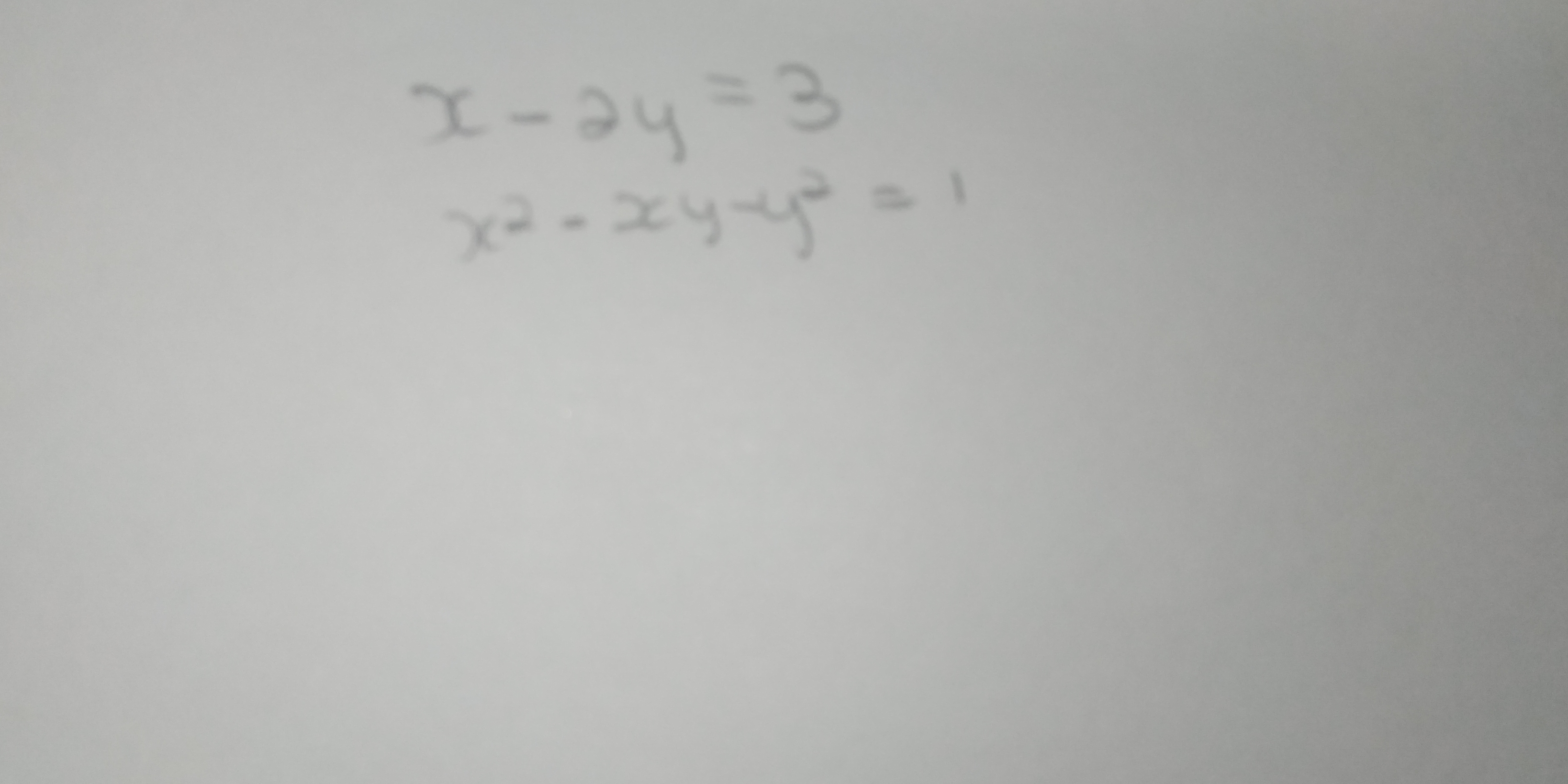
Understand the Problem
The question presents a system of two equations with two variables, x and y. The first equation is linear, and the second is a quadratic equation. The goal is to find the values of x and y that satisfy both equations simultaneously by solving the system of equations.
Answer
$(1, -1)$ and $(-13, -8)$
Answer for screen readers
$(1, -1)$ and $(-13, -8)$
Steps to Solve
-
Solve the first equation for x Solve the first equation for $x$ in terms of $y$. $x - 2y = 3$ $x = 2y + 3$
-
Substitute into the second equation Substitute $x = 2y + 3$ into the second equation $x^2 - xy - y^2 = 1$. $(2y + 3)^2 - (2y + 3)y - y^2 = 1$
-
Expand and simplify Expand and simplify the equation. $4y^2 + 12y + 9 - 2y^2 - 3y - y^2 = 1$ $y^2 + 9y + 9 = 1$ $y^2 + 9y + 8 = 0$
-
Solve for y Solve the quadratic equation for $y$. $y^2 + 9y + 8 = 0$ $(y + 1)(y + 8) = 0$ $y = -1$ or $y = -8$
-
Solve for x when y = -1 Substitute $y = -1$ into $x = 2y + 3$. $x = 2(-1) + 3$ $x = -2 + 3$ $x = 1$
-
Solve for x when y = -8 Substitute $y = -8$ into $x = 2y + 3$. $x = 2(-8) + 3$ $x = -16 + 3$ $x = -13$
-
Solutions The solutions are $(1, -1)$ and $(-13, -8)$.
$(1, -1)$ and $(-13, -8)$
More Information
We found two pairs of $x$ and $y$ values that satisfy both equations. These are the points where the line and hyperbola intersect.
Tips
A common mistake is to make an error in the expansion or simplification of the equations, especially when substituting and expanding the quadratic equation. Another common mistake is to forget to solve for $x$ after finding the values of $y$, or to mix up the corresponding $x$ and $y$ values.
AI-generated content may contain errors. Please verify critical information