Make m the subject of the formula p = (m/(a+m))^(1/3)
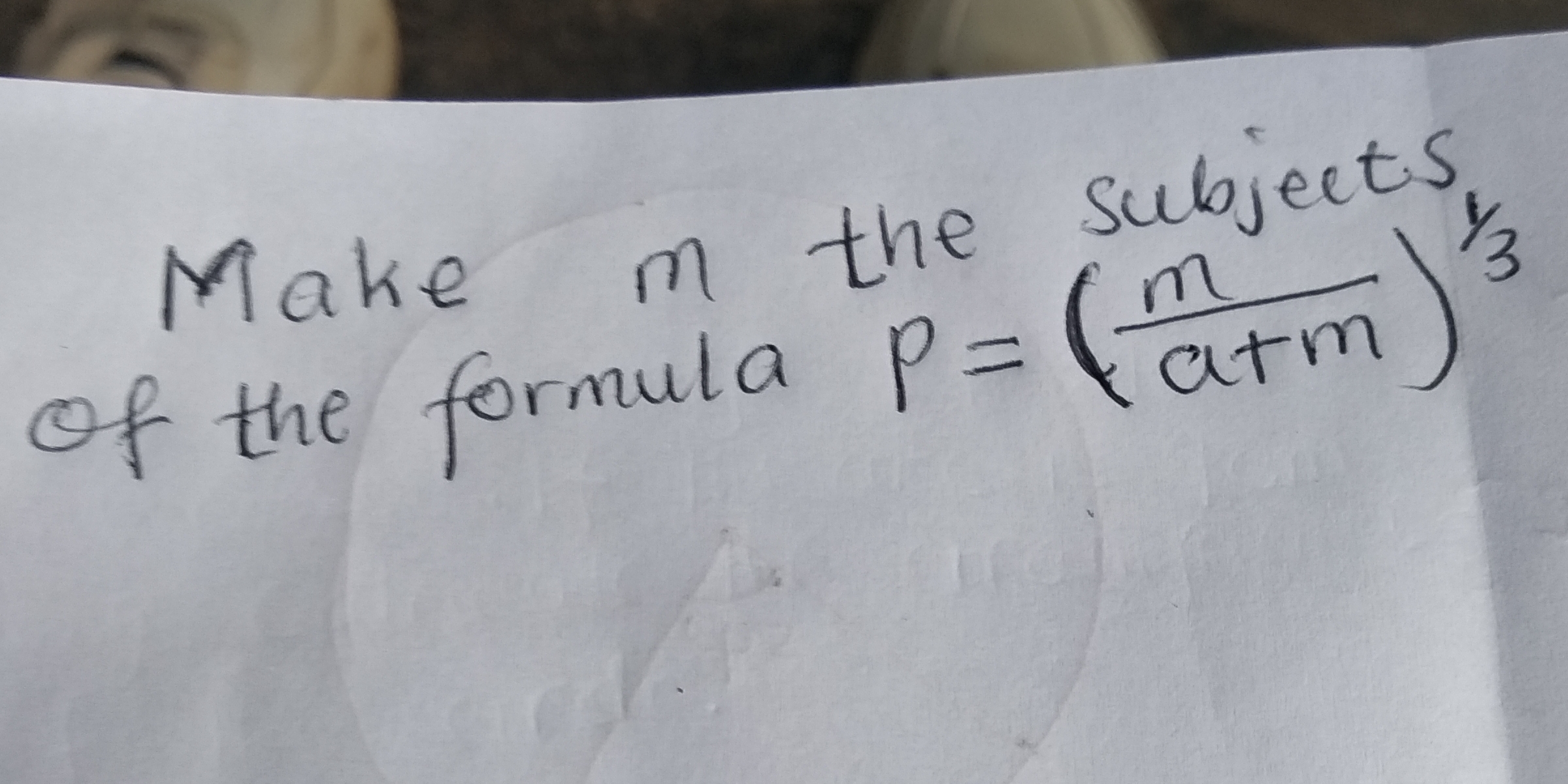
Understand the Problem
The question asks us to rearrange the formula (p = (\frac{m}{a+m})^{\frac{1}{3}}) to make (m) the subject.
Answer
$m = \frac{ap^3}{1-p^3}$
Answer for screen readers
$m = \frac{ap^3}{1-p^3}$
Steps to Solve
- Raise both sides to the power of 3
To eliminate the cube root, raise both sides of the equation to the power of 3:
$p^3 = (\frac{m}{a+m})^{\frac{1}{3} \cdot 3}$
$p^3 = \frac{m}{a+m}$
- Multiply both sides by (a+m)
Multiply both sides by $(a+m)$ to get rid of the fraction:
$p^3(a+m) = m$
- Expand the left side
Expand the left side of the equation:
$p^3a + p^3m = m$
- Rearrange the equation
Move terms containing $m$ to one side:
$p^3a = m - p^3m$
- Factor out m
Factor out $m$ from the right side:
$p^3a = m(1 - p^3)$
- Solve for m
Divide both sides by $(1 - p^3)$ to isolate $m$:
$m = \frac{p^3a}{1 - p^3}$
$m = \frac{ap^3}{1-p^3}$
More Information
The formula $m = \frac{ap^3}{1-p^3}$ expresses $m$ in terms of $a$ and $p$.
Tips
A common mistake is not distributing $p^3$ correctly when multiplying it by $(a+m)$. Also, errors can occur when rearranging the terms to isolate $m$.
AI-generated content may contain errors. Please verify critical information